题目内容
(本小题满分12分)已知向量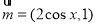 ,
,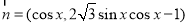 ,函数
,函数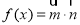 .
.
(1)求函数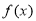 的单调递增区间;
的单调递增区间;
(2)在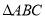 中,角
中,角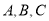 的对边分别为
的对边分别为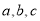 ,若
,若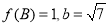 ,
, ,求
,求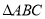
的面积.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)首先根据平面向量数量积的坐标运算得到 的表达式,再由二倍角公式的降幂变形以及辅助角公式将
的表达式,再由二倍角公式的降幂变形以及辅助角公式将 的表达式进行化简,从而可得
的表达式进行化简,从而可得 ,再由正弦函数
,再由正弦函数 的单调性,可知要求
的单调性,可知要求 的单调递增区间,只需令
的单调递增区间,只需令 ,即可得
,即可得 的单调递增区间为
的单调递增区间为 ;(2)由(1)及条件
;(2)由(1)及条件 可得
可得 ,再由正弦定理可将条件
,再由正弦定理可将条件 变形为
变形为 ,再结合余弦定理
,再结合余弦定理 ,联立方程组即可解得
,联立方程组即可解得 ,
, ,从而
,从而 .
.
试题解析:(1)∵ ,
,
∴ ,令
,令 ,
, ∴
∴ ,
,
∴函数 的单调递增区间为
的单调递增区间为 ;(2)∵
;(2)∵ ,
,
∴ ,∴
,∴ ,∵
,∵ ,∴
,∴ ,
,
又∵ ,
, , ∴
, ∴ ,
, , ∴
, ∴ .
.
考点:1.三角恒等变形;2.函数 的性质;3.正余弦定理解三角形.
的性质;3.正余弦定理解三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
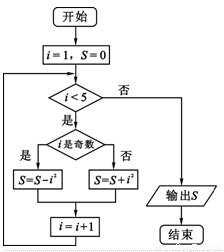
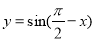 的图象 ( )
的图象 ( )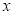 轴对称 (B)关于
轴对称 (B)关于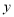 轴对称
轴对称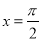 对称
对称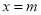 和
和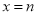 是函数
是函数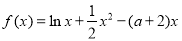 的两个极值点,其中
的两个极值点,其中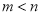 ,
,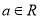 .
.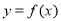 在点
在点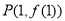 处的切线垂直于
处的切线垂直于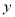 轴,求实数
轴,求实数 的值;
的值;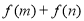 的取值范围;
的取值范围;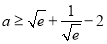 ,求
,求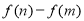 的最大值(
的最大值(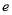 是自然对数的底数).
是自然对数的底数). ,则
,则 ___________.
___________.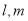 和平面
和平面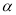 ,则下列命题正确的是( )
,则下列命题正确的是( )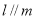 ,
, ,则
,则
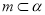 ,则
,则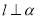 ,
,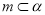 ,则
,则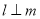
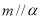
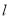 上有无数个点不在平面
上有无数个点不在平面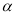 内,则
内,则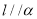 ;
;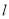 与平面
与平面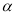 平行,则
平行,则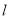 与平面
与平面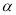 内的任意一条直线都平行;
内的任意一条直线都平行;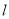 与平面
与平面 B.
B.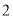 C.
C.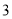 D.
D.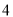
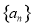 中,已知
中,已知 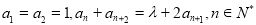 ,
,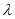 为常数.
为常数.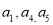 成等差数列;
成等差数列;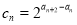 ,求数列 的前n项和
,求数列 的前n项和 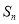 ;
;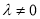 时,数列
时,数列 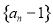 中是否存在三项
中是否存在三项 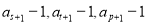 成等比数列,且
成等比数列,且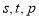 也成等比数列?若存在,求出
也成等比数列?若存在,求出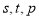 的值;若不存在,说明理由.
的值;若不存在,说明理由.