题目内容
7.如图所示,已知$\overrightarrow{AC}=3\overrightarrow{BC}$,$\overrightarrow{OA}$=$\overrightarrow a$,$\overrightarrow{OB}$=$\overrightarrow b$,$\overrightarrow{OC}$=$\overrightarrow c$,则下列等式中成立的是( )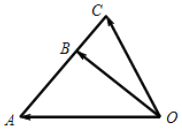
| A. | $\overrightarrow c=\frac{3}{2}\overrightarrow b-\frac{1}{2}\overrightarrow a$ | B. | $\overrightarrow c=2\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow c=2\overrightarrow a-\overrightarrow b$ | D. | $\overrightarrow c=\frac{3}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ |
分析 利用向量的三角形法则,把$\overrightarrow{OA}、\overrightarrow{OB}$作为基底进行加法运算.
解答 解:$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC}=\overrightarrow{OA}+\frac{3}{2}\overrightarrow{AB}$
=$\overrightarrow{OA}+\frac{3}{2}(\overrightarrow{OB}-\overrightarrow{OA})$
=$\frac{3}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OA}$
=$\frac{3}{2}\overrightarrow{b}-\frac{1}{2}\overrightarrow{a}$.
故选:A.
点评 本题考查了平面向量的加法运算法则,属于基础题.

练习册系列答案
相关题目
18.已知菱形ABCD的边长为2,E为AB的中点,∠ABC=120°,则$\overrightarrow{DE}$•$\overrightarrow{BD}$的值为( )
| A. | 3 | B. | -3 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
12.若实数x、y满足|x|≤y≤1,则x2+y2+2x的最小值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$-1 |
16.设i为虚数单位,复数$z=\frac{1-i}{3-i}$的虚部是( )
| A. | $\frac{1}{5}$ | B. | $-\frac{1}{5}$ | C. | 1 | D. | -1 |
 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且经过点$(0,\;-2\sqrt{2})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且经过点$(0,\;-2\sqrt{2})$,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P.