题目内容
3.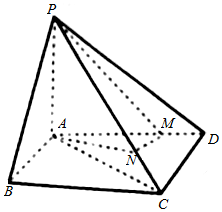 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4.(Ⅰ)求证:MN∥平面PAB;
(Ⅱ)求三棱锥P-AMN的体积.
分析 (I)在AC上取一点Q,使得$\frac{AQ}{QC}=4$,则MQ∥AB,NQ∥PA,故平面MNQ∥平面PAB,于是MN∥平面PAB;
(II)过C作CH⊥AD,垂足为H,计算CH,则N到平面PAD的距离h=$\frac{4}{5}CH$,代入棱锥的体积公式V=$\frac{1}{3}{S}_{△PAM}•h$计算即可.
解答 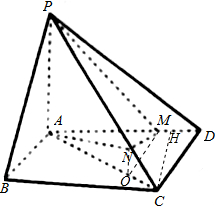 (Ⅰ)证明:在AC上取一点Q,使得$\frac{AQ}{QC}=4$,连接MQ,QN,
(Ⅰ)证明:在AC上取一点Q,使得$\frac{AQ}{QC}=4$,连接MQ,QN,
则$\frac{AM}{MD}=\frac{AQ}{QC}=\frac{PN}{NC}$,∴QN∥AP,MQ∥CD,
又CD∥AB,
∴MQ∥AB.
又∵AB?平面PAB,PA?平面PAB,MQ?平面MNQ,
NQ?平面MNQ
∴平面PAB∥平面MNQ,
又∵MN?平面MNQ,MN?平面PAB,
∴MN∥平面PAB.
(Ⅱ)解:∵AB=3,BC=5,AC=4,
∴AB⊥AC.
过C作CH⊥AD,垂足为H,则CH=$\frac{3×4}{5}$=$\frac{12}{5}$,
∵PA⊥平面ABCD,CH?平面ABCD,
∴PA⊥CH,又CH⊥AD,PA∩AD=A,PA?平面PAD,AD?平面PAD,
∴CH⊥平面PAD,
∵PC=$\sqrt{P{A}^{2}+A{C}^{2}}$=$\sqrt{41}$,$\frac{PN}{NC}=4$,
∴N到平面PAD的距离h=$\frac{4}{5}$CH=$\frac{48}{25}$,
∴VP-AMN=VN-PAM=$\frac{1}{3}{S}_{△PAM}•h$=$\frac{1}{3}×\frac{1}{2}×5×4×\frac{48}{25}$=$\frac{32}{5}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于中档题.

| A. | (2,3] | B. | [2,3] | C. | (2,3) | D. | [2,3) |
| A. | 3 | B. | -3 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$-1 |
