题目内容
7.已知tanα=$\sqrt{2}$,α为第三象限角,则$\sqrt{2}$sinα+cosα=( )| A. | -$\sqrt{2}$ | B. | -2$\sqrt{2}$ | C. | -$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
分析 利用同角三角函数基本关系式,求解处sinα和cosα的值可得答案.
解答 解:由tanα=$\sqrt{2}$,得sinα=$\sqrt{2}$cosα,sin2α+cos2α=1,可得cos2α=$\frac{1}{3}$,
又α为第三象限角,∴$cosα=-\frac{\sqrt{3}}{3}$
∴$\sqrt{2}$sinα+cosα=3cosα=-$\sqrt{3}$
故选C.
点评 本题考查了“弦化切”及同角三角函数基本关系式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
19.(理)若a=${∫}_{\frac{π}{2}}^{2}$sinxdx,b=∫01cosxdx,则a与b的关系是( )
| A. | a+b=0 | B. | a>b | C. | a<b | D. | a=b |
16.已知倾斜角为α的直线l与直线x+2y-4=0垂直,则$cos(\frac{2017}{2}π-2α)$的值为( )
| A. | 2 | B. | $-\frac{1}{2}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
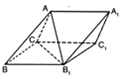 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.