题目内容
17．已知函数f（x）=loga（x-2016）+1（a＞0且，a≠1）的图象恒过定点P，则点P的坐标是（2017，1）．分析 由loga1=0，知x-2016=1，即x=2017时，y=1，由此能求出点P的坐标．
解答 解：∵loga1=0，
∴x-2016=1，即x=2017时，y=1，
∴点P的坐标是P（2017，1）．
故答案为：（2017，1）．
点评 本题考查对数函数的性质和特殊点，解题时要认真审题，仔细解答，避免出错．
练习册系列答案
相关题目
7．已知tanα=$\sqrt{2}$，α为第三象限角，则$\sqrt{2}$sinα+cosα=（ ）
| A． | -$\sqrt{2}$ | B． | -2$\sqrt{2}$ | C． | -$\sqrt{3}$ | D． | -2$\sqrt{3}$ |
8．$\frac{1-2i}{2+i}$=（ ）
| A． | -i | B． | i | C． | 1 | D． | 2-i |
5．若双曲线$\frac{{x}^{2}}{16+k}$-$\frac{{y}^{2}}{8-k}$=1（-16＜k＜8）的一条渐近线方程是y=-$\sqrt{3}$x，点P（3，y0）与点Q是双曲线上关于坐标原点对称的两点，则四边形F1QF2P的面积是．
| A． | 12$\sqrt{6}$ | B． | 6$\sqrt{6}$ | C． | 12$\sqrt{2}$ | D． | 6$\sqrt{2}$ |
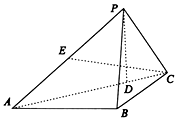如图，在三棱锥P-ABC中，PA⊥PC，PB=AB=BC=2，∠ABC=120°，$PC=\sqrt{3}$，D为AC上一点，且AD=3DC．