题目内容
设全集为R,集合A={x|2x2-7x+3≥0},f(x)=
的定义域为集合B,求A∩B和A∪B.
|
考点:交集及其运算,并集及其运算
专题:计算题
分析:分别求出A中不等式的解集确定出A,求出B中函数的定义域确定出B,找出A与B的交集及并集即可.
解答:
解:由2x2-7x+3≥0得:x≤
或x≥3,即A={x|x≤
或x≥3},
由
-2≥0,得:
≥0,
解得:-1<x≤1,即B={x|-1<x≤1},
∴A∩B={x|-1<x≤
},A∪B={x|x≤1或x≥3}.
| 1 |
| 2 |
| 1 |
| 2 |
由
| x+3 |
| x+1 |
| -x+1 |
| x+1 |
解得:-1<x≤1,即B={x|-1<x≤1},
∴A∩B={x|-1<x≤
| 1 |
| 2 |
点评:此题考查了交、并集及其运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
已知两圆的半径分别为7和1,当它们内切时,圆心距为( )
| A、6 | B、7 | C、8 | D、9 |
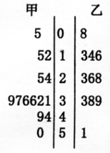 如图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图,则甲运动员的得分的中位数是
如图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图,则甲运动员的得分的中位数是 在三棱锥A-BCD中,AB⊥AC,AB⊥AD,AC⊥AD,AB=AC=1,AD=2,E、F分别是BC、BD的中点.
在三棱锥A-BCD中,AB⊥AC,AB⊥AD,AC⊥AD,AB=AC=1,AD=2,E、F分别是BC、BD的中点.