题目内容
3.已知tanα=-4,求下列各式的值:(1)sin2α;
(2)3sinαcosα;
(2)cos2α-sin2α;
(4)$\frac{4sinα-2cosα}{3sinα+5cosα}$.
分析 利用同角的三角函数基本关系式,把正弦、余弦化为正切函数,计算即可.
解答 解:(1)sin2α=$\frac{{sin}^{2}α}{{sin}^{2}α{+cos}^{2}α}$=$\frac{{tan}^{2}α}{{tan}^{2}α+1}$=$\frac{{(-4)}^{2}}{{(-4)}^{2}+1}$=$\frac{16}{17}$;
(2)3sinαcosα=$\frac{3sinαcosα}{{sin}^{2}α{+cos}^{2}α}$=$\frac{3tanα}{{tan}^{2}α+1}$=$\frac{3×(-4)}{{(-4)}^{2}+1}$=-$\frac{12}{17}$;
(3)cos2α-sin2α=$\frac{{cos}^{2}α{-sin}^{2}α}{{sin}^{2}α{+cos}^{2}α}$=$\frac{1{-tan}^{2}α}{{tan}^{2}α+1}$=$\frac{1{-(-4)}^{2}}{{(-4)}^{2}+1}$=-$\frac{15}{17}$;
(4)$\frac{4sinα-2cosα}{3sinα+5cosα}$=$\frac{4tanα-2}{3tanα+5}$=$\frac{4×(-4)-2}{3×(-4)+5}$=$\frac{18}{7}$.
点评 本题考查了同角的三角函数基本关系式以及正弦、余弦化为正切函数的应用问题,是基础题目.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
13.已知函数f(x)=$\left\{\begin{array}{l}{sinx+2cos2x,x≥0}\\{-{e}^{2x},x<0}\\{\;}\end{array}\right.$,则f(f($\frac{π}{2}$))等于( )
| A. | -$\frac{1}{{e}^{2}}$ | B. | $\frac{1}{{e}^{2}}$ | C. | -e2 | D. | e2 |
9.根据二分法原理求解方程x2-4=0得到的框图可称为( )
| A. | 知识结构图 | B. | 组织结构图 | C. | 工序流程图 | D. | 程序流程图 |
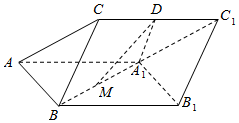 如图,三棱柱ABC-A1B1C1中,D,M分别为CC1,A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,D,M分别为CC1,A1B的中点,A1D⊥CC1,△AA1B是边长为2的正三角形,A1D=2,BC=1.