题目内容
8.在△ABC中,已知atanA+btanB=(a+b)tan$\frac{A+B}{2}$,试判断此三角形的形状.分析 根据正弦定理以及两角和与差的正弦公式,同角的三角函数的关系,化简即可.
解答 解:∵atanA+btanB=(a+b)tan$\frac{A+B}{2}$,
∴a(tanA-tan$\frac{A+B}{2}$)=b(tan$\frac{A+B}{2}$-tanB)
∴a($\frac{sinA}{cosA}$-$\frac{sin\frac{A+B}{2}}{cos\frac{A+B}{2}}$)=b($\frac{sin\frac{A+B}{2}}{cos\frac{A+B}{2}}$-$\frac{sinB}{cosB}$),
∴a•$\frac{sin(A-\frac{A+B}{2})}{cos\frac{A+B}{2}cosA}$=b•$\frac{sin(\frac{A+B}{2}-B)}{cos\frac{A+B}{2}cosB}$,
∴a•$\frac{sin\frac{A-B}{2}}{cosA}$=b•$\frac{sin\frac{A-B}{2}}{cosB}$,
∴tanA=tanB,
∴A=B
故三角形为等腰三角形.
点评 本题考查了正弦定理以及两角和与差的正弦公式,同角的三角函数的关系,属于中档题.

练习册系列答案
相关题目
18.若函数f(x)的导函数f′(x)的图象如图所示.则( )
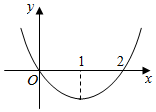

| A. | x=1是最小值点 | B. | x=0是极小值点 | ||
| C. | x=2是极小值点 | D. | 函数f(x)在(1,2)上单调递增 |
16.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,-4),|$\overrightarrow{c}$|=$\sqrt{10}$,且$\overrightarrow{b}$•$\overrightarrow{c}$=$5\sqrt{2}$,则$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
20.在下列函数中,以π为最小正周期,且在(0,$\frac{π}{2}$)内是增函数的是( )
| A. | y=sin$\frac{x}{2}$ | B. | y=cos2x | C. | y=sin(2x+$\frac{π}{4}$) | D. | y=tan(x-$\frac{π}{4}$) |