Question

14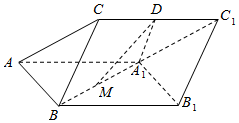．如图，三棱柱ABC-A₁B₁C₁中，D，M分别为CC₁，A₁B的中点，A₁D⊥CC₁，△AA₁B是边长为2的正三角形，A₁D=2，BC=1．
（1）证明：MD∥平面ABC；
（2）证明：BC⊥平面ABB₁A₁．

Answer 1

分析 （1）取AB的中点H，连接HM，CH，根据线面平行的判定定理即可证明MD∥平面ABC；
（2）根据三角形的边长关系证明三角形是直角三角形，然后结合线面垂直的判定定理即可证明BC⊥平面ABB₁A₁．

解答 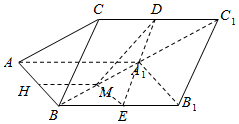证明：（1）取AB的中点H，连接HM，CH，
∵D、M分别为CC₁和A₁B的中点
∴HM∥BB₁，HM=$\frac{1}{2}$BB₁=CD，
∴HM∥CD，HM=CD，
则四边形CDMH是平行四边形，
则CH=DM．
∵CH?平面ABC，DM?平面ABC，
∴MD∥平面ABC；
（2）取BB₁的中点E，
∵△AA₁B是边长为2的正三角形，A₁D=2，BC=1．
∴C₁D=1，
∵A₁D⊥CC₁，
∴A₁C₁=$\sqrt{{2}^{2}+1}$=$\sqrt{5}$，
则A₁B₁²+A₁B₁²=4+1=5=A₁C₁²，
则△A₁B₁C₁是直角三角形，
则B₁C₁⊥A₁B₁，
∵在正三角形BA₁B₁中，A₁E=$\sqrt{3}$，
∴A₁E²+DE²=3+1=4=A₁D₁²，
则△A₁DE是直角三角形，
则DE⊥A₁E，
即BC⊥A₁E，BC⊥A₁B₁，
∵A₁E∩A₁B₁=A₁，
∴BC⊥平面ABB₁A₁．

点评 本题主要考查面面垂直，线面平行的判定，考查了空间想象能力和推理论证能力，综合性较强，属于中档题．