题目内容
18.3${\;}^{lo{g}_{3}5}$+(2005)0-($\frac{1}{4}$)${\;}^{-\frac{1}{2}}$+sin$\frac{7π}{6}$=$\frac{7}{2}$.分析 根据对数的运算性质和指数幂的运算性质,以及特殊角的三角函数值,计算即可.
解答 解:3${\;}^{lo{g}_{3}5}$+(2005)0-($\frac{1}{4}$)${\;}^{-\frac{1}{2}}$+sin$\frac{7π}{6}$=5+1-2-$\frac{1}{2}$=$\frac{7}{2}$,
故答案为:$\frac{7}{2}$.
点评 本题考查了对数的运算性质和指数幂的运算性质,属于基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
4.已知f(x)是定义在R上的不恒等于0的偶函数,且对于任意实数x都有xf(x+1)=(x+1)f(x),则$f(\frac{9}{2})$的值为( )
| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{9}{2}$ |
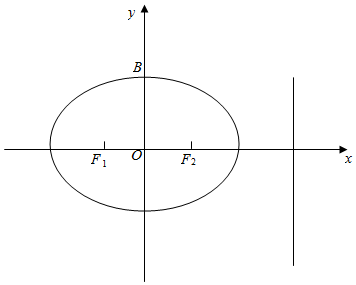 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点B(0,$\sqrt{3}$)是椭圆E的上顶点,F1,F2分别是椭圆E的左、右焦点.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点B(0,$\sqrt{3}$)是椭圆E的上顶点,F1,F2分别是椭圆E的左、右焦点.