题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}{sinx+2cos2x,x≥0}\\{-{e}^{2x},x<0}\\{\;}\end{array}\right.$,则f(f($\frac{π}{2}$))等于( )| A. | -$\frac{1}{{e}^{2}}$ | B. | $\frac{1}{{e}^{2}}$ | C. | -e2 | D. | e2 |
分析 直接利用分段函数,由里及外逐步求解即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{sinx+2cos2x,x≥0}\\{-{e}^{2x},x<0}\\{\;}\end{array}\right.$,则f($\frac{π}{2}$)=sin$\frac{π}{2}$+2cosπ=1-2=-1.
f(f($\frac{π}{2}$))=f(-1)=-e-2.
故选:A.
点评 本题考查分段函数的应用,三角函数化简求值,考查计算能力.

练习册系列答案
相关题目
3.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(4-x),x<4}\\{1+{2}^{x-1},x≥4}\end{array}\right.$,则f(0)+f(log232)=( )
| A. | 19 | B. | 17 | C. | 15 | D. | 13 |
18.若函数f(x)的导函数f′(x)的图象如图所示.则( )
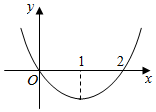

| A. | x=1是最小值点 | B. | x=0是极小值点 | ||
| C. | x=2是极小值点 | D. | 函数f(x)在(1,2)上单调递增 |
2.在一个二面角的两个面内都和二面角的棱垂直的两个向量分别为(0,-1,3),(2,2,4),则这个二面角的余弦值为( )
| A. | $\frac{\sqrt{15}}{6}$ | B. | -$\frac{\sqrt{15}}{6}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | 以上都不对 |