题目内容
求由两条曲线y=-x2,4y=-x2及直线y=-1所围成图形的面积,并画出简图.
考点:定积分在求面积中的应用
专题:计算题,导数的概念及应用
分析:由图形的对称性知,所求图形面积为位于y轴右侧图形面积的2倍.联立方程,组成方程组,求得交点坐标,可得被积区间,再用定积分表示出封闭图形的面积,即可求得结论.
解答:
解: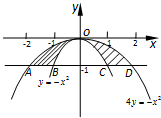 由图形的对称性知,所求图形面积为位于y轴右侧图形面积的2倍.
由图形的对称性知,所求图形面积为位于y轴右侧图形面积的2倍.
由
得C(1,-1).
同理得D(2,-1).
∴所求图形的面积S=2{
[-
-(-x2)]dx+
[-
-(-1)]dx}
=2(
dx-
dx+
dx)=2(
-
+x
)=
.
 由图形的对称性知,所求图形面积为位于y轴右侧图形面积的2倍.
由图形的对称性知,所求图形面积为位于y轴右侧图形面积的2倍.由
|
同理得D(2,-1).
∴所求图形的面积S=2{
| ∫ | 1 0 |
| x2 |
| 4 |
| ∫ | 2 1 |
| x2 |
| 4 |
=2(
| ∫ | 1 0 |
| 3x2 |
| 4 |
| ∫ | 2 1 |
| x2 |
| 4 |
| ∫ | 2 1 |
| x3 |
| 4 |
| | | 1 0 |
| x3 |
| 12 |
| | | 2 1 |
| | | 2 1 |
| 4 |
| 3 |
点评:本题考查利用定积分求面积,解题的关键是确定被积区间及被积函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若实数x,y满足不等式组
且x+y的最大值为6,则实数m=( )
|
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
 如图,已知连接椭圆
如图,已知连接椭圆