题目内容
已知函数f(x)=ax-lnx,在点x=1处切线方程为y=2x+b,求实数a,b的值.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出函数的导数,求出切线的斜率,再由切线方程得到斜率,解方程求得a=3,再代入切线方程,得到b.
解答:
解:x=1时,y=a,切点坐标(1,a)
而y=ax-lnx的导数为y′=a-
,
则在点(1,a)处的切线斜率为a-1,
由于在点(1,a)处的切线方程为y=2x+b,
则有a-1=2,可得a=3,
点(1,3)在切线方程y=2x+b上,
则3=2×1+b,
解得b=1.
实数a,b的值分别为:3,1.
而y=ax-lnx的导数为y′=a-
| 1 |
| x |
则在点(1,a)处的切线斜率为a-1,
由于在点(1,a)处的切线方程为y=2x+b,
则有a-1=2,可得a=3,
点(1,3)在切线方程y=2x+b上,
则3=2×1+b,
解得b=1.
实数a,b的值分别为:3,1.
点评:本题考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,考查运算能力,属于中档题.

练习册系列答案
相关题目
当y=f(x)是下列的( )时,f′(x)一定是增函数.
| A、二次函数 | B、反比例函数 |
| C、对数函数 | D、指数函数 |
函数y=
-2x的导数是( )
| 2x2+1 |
| x |
A、2-
| ||
B、-
| ||
C、x-
| ||
D、
|
已知全集U=R,集合A={x|x<3},B={x|lnx<0},则A∩∁UB( )
| A、{x|1<x<3} |
| B、{x|x≤0或1≤x<3} |
| C、{x|x<3} |
| D、{x|1≤x<3} |
若sinx+siny=1,则cosx+cosy的取值范围是( )
| A、[-2,2] | ||||
| B、[-1,1] | ||||
C、[0,
| ||||
D、[-
|
已知m>0,n>0,且2m,
,3n成等差数列,则m+
+
+
n的最小值为( )
| 5 |
| 2 |
| 2 |
| m |
| 3 |
| n |
| 3 |
| 2 |
A、
| ||
| B、5 | ||
C、
| ||
| D、15 |
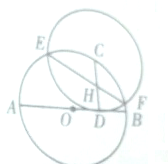 如图所示,在圆O上任取C点为圆心,作一圆C与圆O的直径AB相切于D,圆C与圆O交于E,F,且EF与CD相交于H.求证:EF平分CD.
如图所示,在圆O上任取C点为圆心,作一圆C与圆O的直径AB相切于D,圆C与圆O交于E,F,且EF与CD相交于H.求证:EF平分CD.