题目内容
已知椭圆 的离心率为
的离心率为 ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线 的焦点重合,过点
的焦点重合,过点 且不垂直于
且不垂直于 轴直线
轴直线 与椭圆
与椭圆 相交于
相交于 、
、 两点.
两点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)求 的取值范围.
的取值范围.
 的离心率为
的离心率为 ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线 的焦点重合,过点
的焦点重合,过点 且不垂直于
且不垂直于 轴直线
轴直线 与椭圆
与椭圆 相交于
相交于 、
、 两点.
两点.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)求
 的取值范围.
的取值范围.(Ⅰ) ;(Ⅱ)
;(Ⅱ)
 ;(Ⅱ)
;(Ⅱ)
试题分析:(Ⅰ)根据椭圆的短轴端点与双曲线
 的焦点重合,可求得
的焦点重合,可求得 .由离心率
.由离心率 及
及 求
求 .(Ⅱ)设直线
.(Ⅱ)设直线 的方程为
的方程为 ,代入椭圆方程,整理得:
,代入椭圆方程,整理得: 则点
则点 、
、 的横坐标是该方程的两个根.利用根与系数的关系用
的横坐标是该方程的两个根.利用根与系数的关系用 表示出
表示出 ,由此可求得
,由此可求得 的取值范围.
的取值范围.试题解析:(Ⅰ)由题意知
 ,∴
,∴ ,即
,即 2分
2分又双曲线的焦点坐标为
 ,
, , 3分
, 3分∴
 故椭圆的方程为
故椭圆的方程为 6分
6分(Ⅱ)解:由题意知直线
 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为
由
 得:
得: 
由
 得:
得: 7分
7分设
 ,则
,则
∴
 9分
9分
 -
-
 +
+ =
= 11分
11分 ,
, , 13分
, 13分
 即
即 的取值范围是
的取值范围是 15分
15分
练习册系列答案
相关题目
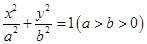 过点(0,4),离心率为
过点(0,4),离心率为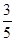
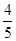 的直线被C所截线段的长度.
的直线被C所截线段的长度.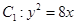 与双曲线
与双曲线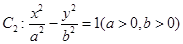 有公共焦点
有公共焦点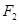 ,点
,点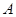 是曲线
是曲线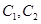 在第一象限的交点,且
在第一象限的交点,且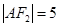 .
.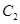 的方程;
的方程;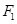 为圆心的圆
为圆心的圆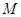 与直线
与直线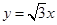 相切,圆
相切,圆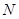 :
: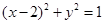 .过点
.过点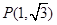 作互相垂直且分别与圆
作互相垂直且分别与圆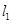 和
和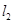 ,设
,设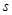 ,
,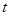 ,问:
,问: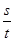 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.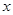 轴上,焦距为
轴上,焦距为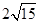 ,且经过点
,且经过点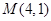 ,直线
,直线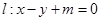 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B.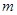 的取值范围;,
的取值范围;,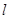 不经过点
不经过点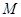 ,求证:直线
,求证:直线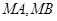 的斜率互为相反数.
的斜率互为相反数.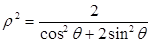 以极点为原点,极轴为
以极点为原点,极轴为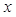 轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.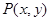 ,求
,求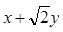 的取值范围;
的取值范围;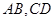 交于点
交于点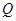 ,且直线
,且直线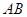 与
与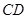 的倾斜角互补,
的倾斜角互补,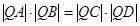 .
.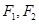 是双曲线
是双曲线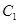 :
: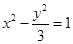 与椭圆
与椭圆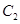 的公共焦点,点A是
的公共焦点,点A是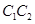 在第一象限的公共点.若
在第一象限的公共点.若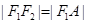 ,则
,则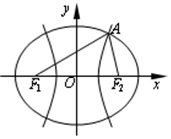
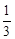
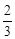
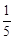
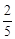
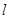 双曲线
双曲线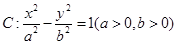 交
交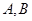 两点,若点
两点,若点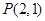 是
是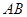 的中点,则
的中点,则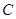 的离心率等于( )
的离心率等于( )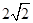
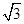
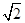
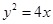 的焦点
的焦点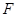 且倾斜角为
且倾斜角为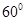 的直线
的直线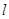 与抛物线在第一、四象限分别交于
与抛物线在第一、四象限分别交于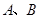 两点,则
两点,则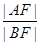 等于( )
等于( )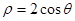 ,曲线C2的参数方程为
,曲线C2的参数方程为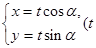 为参数)。
为参数)。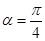 时,求曲线Cl与C2公共点的直角坐标;
时,求曲线Cl与C2公共点的直角坐标; 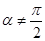 ,当
,当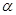 变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.
变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.