题目内容
极坐标系中椭圆C的方程为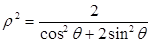 以极点为原点,极轴为
以极点为原点,极轴为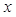 轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(Ⅰ)求该椭圆的直角标方程;若椭圆上任一点坐标为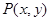 ,求
,求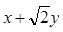 的取值范围;
的取值范围;
(Ⅱ)若椭圆的两条弦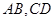 交于点
交于点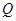 ,且直线
,且直线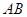 与
与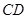 的倾斜角互补,
的倾斜角互补,
求证: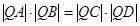 .
.
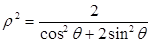 以极点为原点,极轴为
以极点为原点,极轴为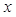 轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.(Ⅰ)求该椭圆的直角标方程;若椭圆上任一点坐标为
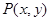 ,求
,求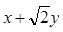 的取值范围;
的取值范围;(Ⅱ)若椭圆的两条弦
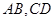 交于点
交于点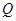 ,且直线
,且直线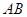 与
与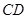 的倾斜角互补,
的倾斜角互补,求证:
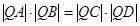 .
.(Ⅰ) (Ⅱ)详见解析
(Ⅱ)详见解析
 (Ⅱ)详见解析
(Ⅱ)详见解析试题分析:将椭圆的极坐标方程转化为一般标准方程,再利用换元法求范围,利用参数方程代入,计算得到结果.
试题解析:(Ⅰ)该椭圆的直角标方程为
 , 2分
, 2分设
 ,
,
所以
 的取值范围是
的取值范围是 4分
4分(Ⅱ)设直线
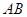 的倾斜角为
的倾斜角为 ,直线
,直线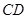 的倾斜角为
的倾斜角为 ,
,
则直线
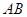 的参数方程为
的参数方程为 (
( 为参数),(5分)
为参数),(5分)代入
 得:
得:
即
 7分
7分同理
 9分
9分所以
 (10分)
(10分)
练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
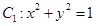 在矩阵
在矩阵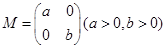 的变换作用下得到曲线
的变换作用下得到曲线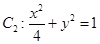 .
.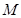 ;
; 的离心率为
的离心率为 ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线 的焦点重合,过点
的焦点重合,过点 且不垂直于
且不垂直于 轴直线
轴直线 与椭圆
与椭圆 相交于
相交于 、
、 两点.
两点. 的取值范围.
的取值范围.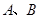 的坐标分别是
的坐标分别是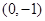 、
、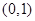 ,直线
,直线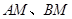 相交于点
相交于点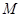 ,且它们的斜率之积为
,且它们的斜率之积为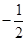 .
.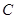 的方程;
的方程;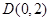 的直线
的直线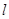 与(1)中的轨迹
与(1)中的轨迹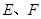 ,试求
,试求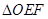 面积的取值范围(
面积的取值范围(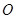 为坐标原点).
为坐标原点).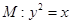 与曲线
与曲线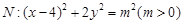 相交于
相交于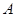 、
、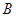 、
、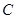 、
、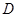 四个点.
四个点.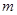 的取值范围;
的取值范围; 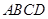 的面积的最大值及此时对角线
的面积的最大值及此时对角线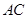 与
与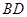 的交点坐标.
的交点坐标.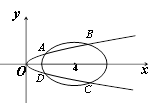

 的左、右焦点分别为
的左、右焦点分别为 ,以
,以 为直径的圆与双曲线渐近线的一个交点为
为直径的圆与双曲线渐近线的一个交点为 ,则此双曲线的方程为( )
,则此双曲线的方程为( )



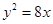 上一点
上一点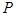 到
到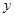 轴的距离是
轴的距离是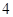 ,则点
,则点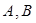 为两个定点,若
为两个定点,若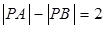 ,则动点
,则动点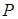 的轨迹为双曲线;
的轨迹为双曲线;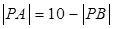 ,且
,且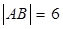 ,则
,则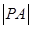 的最大值为8;
的最大值为8;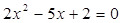 的两根可分别作椭圆和双曲线的离心率;
的两根可分别作椭圆和双曲线的离心率;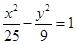 与椭圆
与椭圆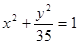 有相同的焦点
有相同的焦点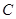 的中心在原点,焦点在
的中心在原点,焦点在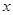 轴上.若椭圆上的点
轴上.若椭圆上的点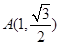 到焦点
到焦点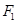 、
、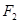 的距离之和等于4.
的距离之和等于4.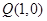 的直线与椭圆交于两点
的直线与椭圆交于两点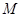 、
、 ,当
,当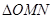 的面积取得最大值时,求直线
的面积取得最大值时,求直线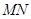 的方程.
的方程.