Question

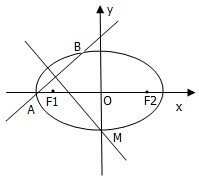已知椭圆Γ：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

3

2

，连接椭圆的四个顶点的菱形面积为4，斜率为k₁的直线l₁与椭圆交于不同的两点A、B，其中A点坐标为（-a，0）．
（1）求椭圆Γ的方程；
（2）若线段AB的垂直平分线与y轴交于点M，当k₁=0时，求

MA

•

MB

的最大值；
（3）设P为椭圆Γ上任意一点，又设过点C（a，0），且斜率为k₂的直线l₂与直线l₁相交于点N，若

1

k1

-

5

k2

=4，求线段PN的最小值．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线的定义、性质与方程

分析：（1）由椭圆的离心率结合菱形面积求得a，b的值，则椭圆方程可求；
（2）设l₁：y=k₁（x+2），代入

x2

4

+y2=1，利用根与系数关系得到AB的中点坐标，求出AB的垂直平分线方程，得到M的坐标，利用向量数量积公式得到数量积关于k₁的关系，换元后利用基本不等式求得

MA

•

MB

的最大值；
（3）设l₂：y=k₂（x-2），联立y=k₁（x+2），得N的坐标，由

1

k1

-

5

k2

=4，得4k₁k₂=k₂-5k₁，进一步得到
∴xN+yN=

2(k1+k2)

k2-k1

+

4k1k2

k2-k1

=3．说明点N在直线x+y=3上运动，求出和x+y=3平行且与

x2

4

+y2=1相切的直线方程，由两点间的距离公式得答案．

解答： 解：（1）由e=

c

a

=

3

2

，得3a²=4c²，
再由c²=a²-b²，解得a=2b．
由题意可知

1

2

×2a×2b=4，即ab=2．
解方程组

a=2b ab=2

，得a=2，b=1．
∴椭圆的方程为

x2

4

+y2=1；
（2）设l₁：y=k₁（x+2），代入

x2

4

+y2=1得，
(1+4k12)x2+16k12x+16k12-4=0．
解得：x=-2或x=

2-8k12

1+4k12

，则B（

2-8k12

1+4k12

，

4k1

1+4k12

），
∴AB的中点为（

-8k12

1+4k12

，

2k1

1+4k12

），
∵k₁≠0，则AB的垂直平分线方程为y-

2k1

1+4k12

=-

1

k1

(x+

8k12

1+4k12

)．
设M（0，y₀），令x=0，得y0=-

6k1

1+4k12

．
则

MA

•

MB

=（-2，-y₀）•（x_B，y_B-y₀）
=-

2(2-8k12)

1+4k12

+

6k1

1+4k12

(

4k1

1+4k12

+

6k1

1+4k12

)
=4[1+

7k12-2

(1+4k12)2

]．
令7k12-2=t＞0，
则

7k12-2

(1+4k12)

=

t

(1+4• t+2 7 )2

=

49

16t+ 225 t +120

≤

49

2 16t• 225 t +120

=

49

240

．
故当t=

15

4

，即k1=±

161

14

时，

MA

•

MB

取最大值4(1+

49

240

)=

289

60

；
（3）设l₂：y=k₂（x-2），联立y=k₁（x+2），得
N（

2(k1+k2)

k2-k1

，

4k1k2

k2-k1

），
由

1

k1

-

5

k2

=4，得4k₁k₂=k₂-5k₁，
∴xN+yN=

2(k1+k2)

k2-k1

+

4k1k2

k2-k1

=3．
故点N在直线x+y=3上运动，
设与x+y=3平行的直线为y=-x+b，
代入

x2

4

+y2=1，得5x²-8bx+4b²-4=0，
由△=0，得b=±

5

．
则PN的最小值为y=-x+

5

与x+y=3的距离，等于

| 5 -3|

2

=

3 2 - 10

2

．

点评：本题是直线与圆锥曲线的综合题，涉及直线与圆锥曲线关系问题，常用直线与曲线联立，根据方程的根与系数的关系求解，但圆锥曲线的特点是计算量比较大，要求考生具备较强的运算推理的能力，是压轴题．