题目内容
设不等式mx2-x+1>0在区间(1,3)上对一切x恒成立,则实数m的取值范围是 .
考点:函数恒成立问题
专题:函数的性质及应用
分析:根据条件,进行参数分离法,结合二次函数的最值是解决本题的关键.
解答:
解:当x∈(1,3)时,不等式mx2-x+1>0恒成立,
即mx2>x-1,
即m>
=
-
设t=
,∵x∈(1,3),∴t∈(
,1).
则y=
-
=t-t2=-(t-
)2+
,
∵t∈(
,1).
∴当t=
时,函数y=t-t2=-(t-
)2+
取得最大值
,
∴m>
,
故答案为:(
,+∞).
即mx2>x-1,
即m>
| x-1 |
| x2 |
| 1 |
| x |
| 1 |
| x2 |
设t=
| 1 |
| x |
| 1 |
| 3 |
则y=
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| 2 |
| 1 |
| 4 |
∵t∈(
| 1 |
| 3 |
∴当t=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴m>
| 1 |
| 4 |
故答案为:(
| 1 |
| 4 |
点评:本题主要考查不等式恒成立问题,利用参数分离法,结合二次函数的性质是解决本题的关键.恒成立的问题一般与最值有关.

练习册系列答案
相关题目
已知双曲线C:x2-y2=m2(m>0),则双曲线C的离心率等于( )
A、
| ||
B、
| ||
| C、2 | ||
D、
|
 已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.
已知,如图,AB是⊙O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E. 某校学生在一次学业水平测试中的数学成绩制成如图所示频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为
某校学生在一次学业水平测试中的数学成绩制成如图所示频率分布直方图,60分以下的人要补考,已知90分以上的有80人,则该校需要补考的人数为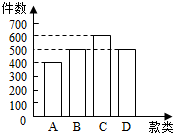 随着社会的发展,网上购物已成为一种新型的购物方式,某商家在网上新推出A,B,C,D四款商品,进行限时促销活动,规定每位注册会员限购一件,并需在网上完成对所购商品的质量评价,以下为四款商品销售情况的条形图和分层抽样法选取100份评价的统计表:
随着社会的发展,网上购物已成为一种新型的购物方式,某商家在网上新推出A,B,C,D四款商品,进行限时促销活动,规定每位注册会员限购一件,并需在网上完成对所购商品的质量评价,以下为四款商品销售情况的条形图和分层抽样法选取100份评价的统计表: