题目内容
18.定义max{a,b}=$\left\{\begin{array}{l}{a,a≥b}\\{b,a<b}\end{array}\right.$,若实数x,y满足$\left\{\begin{array}{l}{-1≤x≤1}\\{-1≤y≤1}\end{array}\right.$,则max{|2x+1|,|x-y+5|}的最小值为3.分析 分析可得当x,y满足$\left\{\begin{array}{l}{-1≤x≤1}\\{-1≤y≤1}\end{array}\right.$时,|2x+1|≤3,|x-y+5|=5+x-y≥3,从而化简max{|2x+1|,|x-y+5|}=5+x-y,从而求最小值.
解答 解:∵当x,y满足$\left\{\begin{array}{l}{-1≤x≤1}\\{-1≤y≤1}\end{array}\right.$时,
|2x+1|≤3,|x-y+5|=5+x-y≥3,
∴max{|2x+1|,|x-y+5|}=5+x-y,
故当x=-1,y=1时,
5+x-y有最小值3,
故答案为:3.
点评 本题考查了分段函数,绝对值函数及分类讨论的思想应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.函数f(x)=$\frac{1}{3}$x3-ax2-3a2x-4在(3,+∞)上是增函数,则实数a的取值范围是( )
| A. | a≥0 | B. | a≥1 | C. | a≤-3或a≥1 | D. | -3≤a≤1 |
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,P是直线x=a上一点,且PF1⊥PF2,|PF1|+|PF2|=2$\sqrt{2}$a,则双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2 | D. | $\sqrt{3}$ |
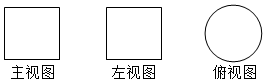 加图所示,一个空间几何体的主视图和左视图都是边长为3的正方形,俯视图是一个直径为3的圆,那么这个几何体的全面积为36π.
加图所示,一个空间几何体的主视图和左视图都是边长为3的正方形,俯视图是一个直径为3的圆,那么这个几何体的全面积为36π.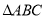 中,
中,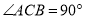 ,
,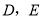 分别为
分别为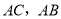 的中点,
的中点,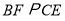 交
交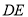 的延长线于点
的延长线于点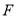 .
.
 是平行四边形;
是平行四边形; 时,求证:四边形
时,求证:四边形