题目内容
设a,b∈R,则a>b是a|a|>b|b|的什么条件 .
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:讨论a,b的取值,去绝对值,从而判断出能够得出a|a|>b|b|成立,并且翻过去由a|a|>b|b|能得到a>b成立,所以得到a>b是a|a|>b|b|的充要条件.
解答:
解:(1)当a≤0时,b<0,则:
a|a|=-a2,b|b|=-b2;
∵a>b;
∴a2<b2;
∴-a2>-b2;
∴a|a|>b|b|;
(2)当a>0,b≤0时,显然a|a|>b|b|成立;
(3)当a>0,b>0时,则:
a|a|=a2,b|b|=b2;
∵a>b;
∴a2>b2;
∴a|a|>b|b|;
反之也成立;
∴a>b是a|a|>b|b|的充要条件.
故答案为:充要条件.
a|a|=-a2,b|b|=-b2;
∵a>b;
∴a2<b2;
∴-a2>-b2;
∴a|a|>b|b|;
(2)当a>0,b≤0时,显然a|a|>b|b|成立;
(3)当a>0,b>0时,则:
a|a|=a2,b|b|=b2;
∵a>b;
∴a2>b2;
∴a|a|>b|b|;
反之也成立;
∴a>b是a|a|>b|b|的充要条件.
故答案为:充要条件.
点评:考查a,b同号时,根据a>b判断a2,b2的关系,以及充分条件、必要条件、充要条件的概念.

练习册系列答案
相关题目
已知集合A={x|-1≤x≤1},B={x|x2-2x≤0},则A∩(∁RB)=( )
| A、[-1,0) |
| B、[-1,0] |
| C、[0,1] |
| D、(-∞,1]∪[2,+∞) |
甲、乙两人在一次射击测试中各射靶10次,如图分别是这两人命中环数的直方图,
若他们的成绩平均数分别为
和
,成绩的标准差分别为s1和s2,则( )

若他们的成绩平均数分别为
. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={x|x≤1},若B⊆A,则集合B可以是( )
| A、{x|x≤2} |
| B、{x|x>1} |
| C、{x|x≤0} |
| D、R |
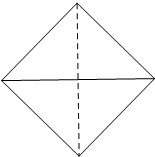 已知四面体S-ABC的所有棱长都相等,它的俯视图是一个边长为
已知四面体S-ABC的所有棱长都相等,它的俯视图是一个边长为 如图是抛物线型拱桥,在平时,水面离拱顶3米,水面宽为2
如图是抛物线型拱桥,在平时,水面离拱顶3米,水面宽为2