题目内容
1．设x，y满足约束条件$\left\{\begin{array}{l}{x+y≤1}\\{y≤x}\\{y≥-2}\end{array}\right.$，则z=3x-y的最大值为（ ）| A． | 1 | B． | -4 | C． | 7 | D． | 11 |
分析 先根据约束条件画出可行域，再利用几何意义求最值，z=3x-y表示直线在y轴上的截距，只需求出可行域直线在y轴上的截距最小值即可．
解答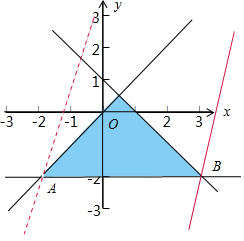 
解：不等式组$\left\{\begin{array}{l}{x+y≤1}\\{y≤x}\\{y≥-2}\end{array}\right.$表示的平面区域如图所示，
当直线z=3x-y过点B时，z=3x-y取得最大值，由$\left\{\begin{array}{l}{y=-2}\\{x+y=1}\end{array}\right.$可得B（3，-2）
在y轴上截距最小，此时z取得最大值11．
故选：D．
点评 本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题．
练习册系列答案
相关题目
11．已知命题p：若x＜-3，则x2-2x-8＞0，则下列叙述正确的是（ ）
| A． | 命题p的逆命题是：若x2-2x-8≤0，则x＜-3 | |
| B． | 命题p的否命题是：若x≥-3，则x2-2x-8＞0 | |
| C． | 命题p的否命题是：若x＜-3，则x2-2x-8≤0 | |
| D． | 命题p的逆否命题是真命题 |
12．定义在R上的函数f（x），已知函数y=f（x+1）的图象关于直线x=-1对称，对任意的x1，x2∈（-∞，0）（x1≠x2），都有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}＜0$，则下列结论正确的是（ ）
| A． | f（0.32）＜f（20.3）＜f（log25） | B． | $f（{log_2}5）＜f（{2^{0.3}}）＜f（{0.3^2}）$ | ||
| C． | $f（{log_2}5）＜f（{0.3^2}）＜f（{2^{0.3}}）$ | D． | $f（{0.3^2}）＜f（{log_2}5）＜f（{2^{0.3}}）$ |
10．某射手进行一次射击，射中环数及相应的概率如下表
（1）根据上表求N的值（2）该射手射击一次射中的环数小于8环的概率
（3）该射手射击一次至少射中8环的概率．
| 环数 | 10 | 9 | 8 | 7 | 7以下 |
| 概率 | 0.25 | 0.3 | 0.2 | 0.15 | N |
（3）该射手射击一次至少射中8环的概率．