题目内容
设a>0,f(x)=
-
是R上的奇函数.
(1)求a的值;
(2)用定义证明:f(x)在(-∞,+∞)上是增函数.
| ex |
| a |
| a |
| ex |
(1)求a的值;
(2)用定义证明:f(x)在(-∞,+∞)上是增函数.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)由定义在R的奇函数图象必过坐标原点,可得f(0)=0,代入可构造关于a的方程,解方程可得答案.
(2)设两个实数数x1、x2∈R,且x1<x2,将f(x1)与f(x2)作差变形整理,得f(x1)<f(x2),由此即可证明函数为减函数.
(2)设两个实数数x1、x2∈R,且x1<x2,将f(x1)与f(x2)作差变形整理,得f(x1)<f(x2),由此即可证明函数为减函数.
解答:
解:(1)若函数f(x)=
-
是R上的奇函数,
则f(0)=
-
=
-a=0,
解得a=1.
(2)∵a=1,∴f(x)=ex-
设x1,x2∈R,x1<x2,则
f(x1)-f(x2)=ex1-
-ex2+
)=ex1-ex2+
-
=ex1-ex2+
=(ex1-ex2 )(1+
),
∵x1<x2,∴ex1<ex2,∴ex1-ex2<0,∵1+
>0,
∴(ex1-ex2 )(1+
)<0,
∴f(x1)-f(x2)<0,
f(x1)<f(x2),∴f(x)在(-∞,+∞)上是增函数.
| ex |
| a |
| a |
| ex |
则f(0)=
| e0 |
| a |
| a |
| e0 |
| 1 |
| a |
解得a=1.
(2)∵a=1,∴f(x)=ex-
| 1 |
| ex |
设x1,x2∈R,x1<x2,则
f(x1)-f(x2)=ex1-
| 1 |
| ex1 |
| 1 |
| ex2 |
| 1 |
| ex2 |
| 1 |
| ex1 |
| ex1-ex2 |
| ex1ex2 |
| 1 |
| ex1ex2 |
∵x1<x2,∴ex1<ex2,∴ex1-ex2<0,∵1+
| 1 |
| ex1ex2 |
∴(ex1-ex2 )(1+
| 1 |
| ex1ex2 |
∴f(x1)-f(x2)<0,
f(x1)<f(x2),∴f(x)在(-∞,+∞)上是增函数.
点评:本题考查的知识点是函数奇偶性的性质,考查了用定义证明函数单调性的知识,熟练掌握奇函数的特性:定义在R的奇函数图象必过坐标原点,是解答的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
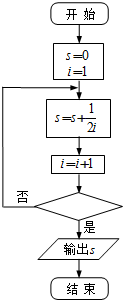 如图给出的是计算
如图给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |
| A、i>8? | B、i>9? |
| C、i>10? | D、i>11? |