题目内容
设f(x)=|sinx|,若x1,x2∈[-
,
],且f(x1)>f(x2),则下列结论成立的是( )
| π |
| 2 |
| π |
| 2 |
| A、x1<x2 |
| B、x1+x2>0 |
| C、x1>x2 |
| D、x12>x22 |
考点:正弦函数的图象
专题:计算题,三角函数的图像与性质
分析:作出f(x)=|sinx|的图象,x1,x2∈[-
,
],由f(x1)>f(x2)即可得到答案.
| π |
| 2 |
| π |
| 2 |
解答:
解:依题意,作出x∈[-
,
]时f(x)=|sinx|的图象,

当x1=
,x2=
时,f(x1)>f(x2),但x1>x2,可排除A;
如图,-
<x1<x2<0时,满足f(x1)>f(x2),可排除C;同时x1+x2<0,可排除B;
故选:D.
| π |
| 2 |
| π |
| 2 |

当x1=
| π |
| 3 |
| π |
| 6 |
如图,-
| π |
| 2 |
故选:D.
点评:本题考查正弦函数的图象,考查作图与分析能力,属于中档题.

练习册系列答案
相关题目
已知集合A={x|0<x<2},B={x|(x-1)(x+1)>0},则A∪B=( )
| A、(0,1) |
| B、(1,2) |
| C、(-∞,-1)∪(0,+∞) |
| D、(-∞,-1)∪(1,+∞) |
函数y=x(x2-1)的大致图象是( )
A、 |
B、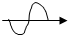 |
C、 |
D、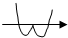 |
 在平面直角坐标系xOy中,点A(0,27
在平面直角坐标系xOy中,点A(0,27 如图是川东地区的行政区划,其中南充、达州各有8个交通
如图是川东地区的行政区划,其中南充、达州各有8个交通