题目内容
选修4-5:不等式选讲
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(Ⅰ)当a=-2时,求不等式f(x)<g(x)的解集;
(Ⅱ)设a>-1,且当x∈[-
,
]时,f(x)<g(x),求a的取值范围.
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(Ⅰ)当a=-2时,求不等式f(x)<g(x)的解集;
(Ⅱ)设a>-1,且当x∈[-
| a |
| 2 |
| 1 |
| 2 |
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用
分析:(Ⅰ)当a=-2时,f(x)<g(x)?|2x-1|+|2x-2|-x-3<0,构造函数函数y=|2x-1|+|2x-2|-x-3,作出其图象,即可求得不等式f(x)<g(x)的解集;
(Ⅱ)当x∈[-
,
),f(x)=1+a,不等式f(x)<g(x)化为1+a≤x+3,依题意,即可求得a的取值范围.
(Ⅱ)当x∈[-
| a |
| 2 |
| 1 |
| 2 |
解答:
解:(I)当a=-2时,不等式f(x)<g(x)化为|2x-1|+|2x-2|-x-3<0.
设函数y=|2x-1|+|2x-2|-x-3,
则y=
,
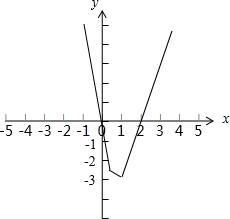
其图象如图,从图象可知,当且仅当x∈(0,2)时,y<0,
∴原不等式的解集是{x|0<x<2};
(Ⅱ)当x∈[-
,
),f(x)=1+a,不等式f(x)<g(x)化为1+a≤x+3,
∴x≥a-2对x∈[-
,
)都成立,故-
≥a-2,即a≤
.
∴a的取值范围是(-1,
].
设函数y=|2x-1|+|2x-2|-x-3,
则y=
|
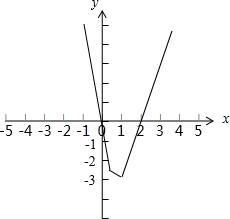
其图象如图,从图象可知,当且仅当x∈(0,2)时,y<0,
∴原不等式的解集是{x|0<x<2};
(Ⅱ)当x∈[-
| a |
| 2 |
| 1 |
| 2 |
∴x≥a-2对x∈[-
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| 4 |
| 3 |
∴a的取值范围是(-1,
| 4 |
| 3 |
点评:本题考查绝对值不等式的解法,着重考查作图分析问题、解决问题的能力,突出恒成立问题的考查,属于中档题.

练习册系列答案
相关题目
把长为1的铁丝截成三段,则这三段恰好能围成三角形的概率是( )
A、
| ||
| B、1 | ||
C、
| ||
D、
|
设f(x)=|sinx|,若x1,x2∈[-
,
],且f(x1)>f(x2),则下列结论成立的是( )
| π |
| 2 |
| π |
| 2 |
| A、x1<x2 |
| B、x1+x2>0 |
| C、x1>x2 |
| D、x12>x22 |
 某种平面分形图如图所示,一级分形图是一个边长为1的等边三角形(图(1));二级分形图是将一级分形图的每条线段三等分,并以中间的那一条线段为一底边向形外作等边三角形,然后去掉底边(图(2));将二级分形图的每条线段三等边,重复上述的作图方法,得到三级分形图(图(3));…;重复上述作图方法,依次得到四级、五级、…、n级分形图.则n级分形图的周长为
某种平面分形图如图所示,一级分形图是一个边长为1的等边三角形(图(1));二级分形图是将一级分形图的每条线段三等分,并以中间的那一条线段为一底边向形外作等边三角形,然后去掉底边(图(2));将二级分形图的每条线段三等边,重复上述的作图方法,得到三级分形图(图(3));…;重复上述作图方法,依次得到四级、五级、…、n级分形图.则n级分形图的周长为 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面A1B1C1,底面为直角三角形,∠ACB=90°,AC=2,BC=1,CC1=
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面A1B1C1,底面为直角三角形,∠ACB=90°,AC=2,BC=1,CC1=