题目内容
试确定m的值,使过点A(m,1),B(-1,m)的直线与过点P(1,2),Q(-5,0)的直线:
(1)平行;
(2)垂直.
(1)平行;
(2)垂直.
考点:直线的一般式方程与直线的平行关系,直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:求出PQ的斜率,(1)通过斜率相等求出m.
(2)利用斜率乘积为-1,求出m的值即可.
(2)利用斜率乘积为-1,求出m的值即可.
解答:
解:过点P(1,2),Q(-5,0)的直线的斜率:
=
(1)两条直线平行,则:
=
,
解得m=
.
(2)两条直线垂直,则:
=-3,解得m=-2.
| 2-0 |
| 1+5 |
| 1 |
| 3 |
(1)两条直线平行,则:
| 1-m |
| m+1 |
| 1 |
| 3 |
解得m=
| 1 |
| 2 |
(2)两条直线垂直,则:
| 1-m |
| m+1 |
点评:本题考查两条直线的平行与垂直条件的应用,基本知识的考查.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
已知复合命题p∧(¬q)是真命题,则下列命题中也是真命题的是( )
| A、(¬p)∨q |
| B、p∨q |
| C、p∧q |
| D、(¬p)∧(¬q) |
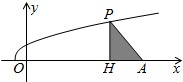 如图,已知点A(11,0),函数y=
如图,已知点A(11,0),函数y=