题目内容
19.在直角坐标系xOy中,圆C1:x2+(y-2)2=$\frac{1}{4}$,椭圆C2:x2+4y2=4,以坐标原点为极点,x轴正半轴为极轴建立极坐标系(I)求C1、C2的极坐标方程;
(Ⅱ)若P,Q分别是圆C1,椭圆C2,椭圆C2上的任意点,求|PQ|的最大值及相应的点Q坐标.
分析 (Ⅰ)由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,能求出圆C1、C2的极坐标方程.
(Ⅱ)设Q(2cosα,sinα),求出P到圆心(0,2)的距离的最大值,由此能求出|PQ|的最大值及相应的Q点坐标.
解答 解:(Ⅰ)∵圆C1:x2+(y-2)2=$\frac{1}{4}$,∴${x}^{2}+{y}^{2}=2y-\frac{15}{4}$,
∴圆C1的极坐标方程为${ρ}^{2}=2ρsinθ-\frac{15}{4}$.
∵椭圆C2:x2+4y2=4,
∴椭圆C2的极坐标方程为ρ2cos2θ+4ρ2sin2θ=4.
(Ⅱ)椭圆C2:x2+4y2=4的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=sinα}\end{array}\right.$,0≤α<2π,
设Q(2cosα,sinα),则P到圆心(0,2)的距离:
d=$\sqrt{4co{s}^{2}α+(2-sinα)^{2}}$=$\sqrt{8-3si{n}^{2}α-4sinα}$=$\sqrt{\frac{28}{3}-3(sinα+\frac{2}{3})^{2}}$≤$\sqrt{\frac{28}{3}}$=$\frac{2\sqrt{21}}{3}$,
当且仅当sinα=-$\frac{2}{3}$时,取等号,此时2cosα=$±\frac{2\sqrt{5}}{3}$.
∴|PQ|的最大值为|PQ|max=$\frac{2\sqrt{21}}{3}+\frac{1}{2}$,此时Q($±\frac{2\sqrt{5}}{3}$,-$\frac{2}{3}$).
点评 本题考查圆的椭圆的极坐标的求法,考查两点间距离的最大值的求法,是中档题,解题时要认真审题,注意两点间距离公式的合理运用.

 阅读快车系列答案
阅读快车系列答案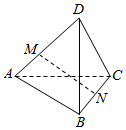
| A. | -$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ | B. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
| A. | [2,+∞) | B. | (2,+∞) | C. | ($\frac{3}{2}$,2] | D. | [$\frac{3}{2}$,2] |
| A. | $\frac{3\sqrt{3}π}{2}$ | B. | 6π | C. | 3π | D. | 3$\sqrt{3}$π |