题目内容
9.直线m:(1+λ)x+y-2λ-4=0与圆O:x2+y2=16交于A,C,直线n:x-(λ+1)(y-2)-2=0与圆O交于B,D,则四边形ABCD面积的最大值是24.分析 先确定直线m,n恒过定点M(2,2),圆心O(0,0),半径R=4,AC2+BD2为定值,表示出面积,即可求四边形ABCD的面积的最大值和最小值.
解答 解:由题意可得,直线m,n恒过定点M(2,2),圆心O(0,0),半径R=4,
设弦AC,BD的中点分别为E,F,则OE2+OF2=OM2=8,
AC=2$\sqrt{16-O{E}^{2}}$,BD=2$\sqrt{16-O{F}^{2}}$,
∴AC2+BD2=4(32-OE2-OF2)=96,
∴S2≤$\frac{1}{4}$AC2•BD2=$\frac{1}{4}$AC2•(96-AC2)≤$\frac{1}{4}•(\frac{A{C}^{2}+96-A{C}^{2}}{2})^{2}$=576,
∴S≤24,当且仅当AC2=96-AC2,即AC=4$\sqrt{3}$时,取等号,
故四边形ABCD面积S的最大值为24.
故答案为:24.
点评 本题主要考查直线过定点,考查面积的计算,基本不等式的应用,正确运用代入法是解题的关键,属于中档题.

练习册系列答案
相关题目
20.在复平面上作出满足下列条件的复数在复平面上对应的点集所表示的图形.
(1)|z|<2;(2)1≤|z|<3;(3)Rez=2;
(4)1<Rez<2且1<lmz<2;(5)|z|>3且lmz<-1.
(1)|z|<2;(2)1≤|z|<3;(3)Rez=2;
(4)1<Rez<2且1<lmz<2;(5)|z|>3且lmz<-1.
4.已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(2015)=3,则f(2016)的值是( )
| A. | -1 | B. | -2 | C. | -3 | D. | 3 |
4.已知双曲线$\frac{x^2}{16}-\frac{y^2}{b^2}=1,(b>0)$实轴的一端点为A,虚轴的一端点为B,且|AB|=5,则该双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{15}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{12}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{3}=1$ |
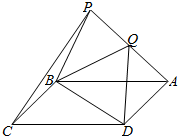 如图所示,点P是平行四边形ABCD所在平面外的一点,点Q是PA的中点,试判断直线PC与平面QBD的位置关系.
如图所示,点P是平行四边形ABCD所在平面外的一点,点Q是PA的中点,试判断直线PC与平面QBD的位置关系.