题目内容
7．已知p：x2-5ax+4a2＜0，其中a＞0，q：3＜x≤4．（1）若a=1，且p∧q为真，求实数x的取值范围；
（2）若p是q的必要不充分条件，求实数a的取值范围．
分析 （1）p：x2-5ax+4a2＜0，其中a＞0，解得：a＜x＜4a；由于a=1，p化为：1＜x＜4．利用p∧q为真，求交集即可得出．
（2）p是q的必要不充分条件，可得q⇒p，且p推不出q，设A=（a，4a），B=（3，4]，则B?A，即可得出．
解答 解：（1）p：x2-5ax+4a2＜0，其中a＞0，解得：a＜x＜4a；q：3＜x≤4．
∵a=1，∴p化为：1＜x＜4．
∵p∧q为真，∴$\left\{\begin{array}{l}{3＜x≤4}\\{1＜x＜4}\end{array}\right.$，解得3＜x≤4，∴实数x的取值范围是（3，4]．
（2）p是q的必要不充分条件，∴q⇒p，且p推不出q，设A=（a，4a），B=（3，4]，
则B?A，
∴$\left\{\begin{array}{l}{a≤3}\\{4＜4a}\end{array}\right.$，解得1＜a≤3．
∴实数a的取值范围是1＜a≤3．
点评 本题考查了不等式的解法、集合的运算性质、简易逻辑的应用，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
17．命题“?x0∈R，x${\;}_{0}^{2}$+2x0≥2”的否定为（ ）
| A． | ?x0∈R，${x}_{0}^{2}$+2x0≤2 | B． | ?x∈R，x2+2x≥2 | ||
| C． | ?x0∈R，${x}_{0}^{2}$+2x0＜2 | D． | ?x∈R，x2+2x＜2 |
2．如图是一个几何体的三视图，则这个几何体的表面积是（ ）
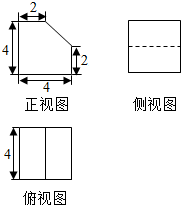
| A． | 84 | B． | $76+8\sqrt{2}$ | C． | $78+8\sqrt{2}$ | D． | $80+8\sqrt{2}$ |
12．
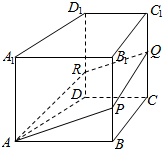如图，在四棱柱ABCD-A1B1C1D1中，AA1⊥平面ABCD，AB∥CD，∠DCB=90°，AB=AD=AA1=2DC，Q为棱CC1上一动点，过直线AQ的平面分别与棱BB1，DD1交于点P，R，则下列结论错误的是（ ）
如图，在四棱柱ABCD-A1B1C1D1中，AA1⊥平面ABCD，AB∥CD，∠DCB=90°，AB=AD=AA1=2DC，Q为棱CC1上一动点，过直线AQ的平面分别与棱BB1，DD1交于点P，R，则下列结论错误的是（ ）| A． | 对于任意的点Q，都有AP∥QR | |
| B． | 对于任意的点Q，四边形APQR不可能为平行四边形 | |
| C． | 存在点Q，使得△ARP为等腰直角三角形 | |
| D． | 存在点Q，使得直线BC∥平面APQR |
19．设全集U={1，2，3，4，5}，集合M={1，4}，N={1，3，5}，则N∩（∁UM）等于（ ）
| A． | {1，3} | B． | {1，5} | C． | {3，5} | D． | {4，5} |