题目内容
6.设P(x,y)满足约束条件$\left\{\begin{array}{l}{x+2y≤4}\\{x+y≤3}\end{array}\right.$,则点P对应的区域与坐标轴围成的封闭图形面积为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{7}{2}$ | D. | $\frac{11}{2}$ |
分析 由约束条件作出可行域,利用两三角形的面积差求得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+2y≤4}\\{x+y≤3}\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{x+y=3}\\{x+2y=4}\end{array}\right.$,解得B(2,1),
则阴影部分的面积为S=S△OAD-S△BCD=$\frac{1}{2}×3×3-\frac{1}{2}×1×2=\frac{7}{2}$.
故选:C.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
16.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-1,m),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则m=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
14.函数f(x)=Asin(ωx+$\frac{ωπ}{2}$)(A>0,ω>0)在区间[-$\frac{3π}{4}$,-$\frac{π}{6}$]上单调递增,则ω的最大值是( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{12}{7}$ | D. | $\frac{12}{11}$ |
 正四棱柱ABCD-A1B1C1D1底面边长为$\sqrt{3}$,高为1,O为下底面的中心.
正四棱柱ABCD-A1B1C1D1底面边长为$\sqrt{3}$,高为1,O为下底面的中心.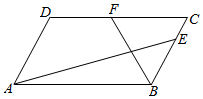 在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=$2\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$$•\overrightarrow{BF}$=( )
在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=$2\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$$•\overrightarrow{BF}$=( )