题目内容
5.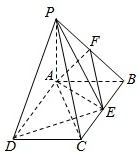 如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.
如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.(Ⅰ)求三棱锥E-PAD的体积;
(Ⅱ)当E是BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅲ)证明:AF⊥PE.
分析 (I)根据棱锥的体积公式计算;
(II)由三角形中位线定理即可证明EF∥PC,从而EF∥平面PAC;
(III)由三线合一可得AF⊥PB,由PA⊥平面ABCD得BC⊥PA,又BC⊥AB,故BC⊥平面PAB,从而由BC⊥AF,于是AF⊥平面PBC,得出AF⊥PE.
解答 解:(Ⅰ)∵PA⊥平面ABCD,底面ABCD是矩形,
∴VE-PAD=VP-ADE=$\frac{1}{3}•{S}_{△ADE}•AP$=$\frac{1}{3}×\frac{1}{2}×2×1×1=\frac{1}{3}$.
(Ⅱ)EF∥平面PAC.
证明:∵E为BC的中点,F是BP的中点,
∴EF∥PC,又∵EF?平面PAC,PC?平面PAC,
∴EF∥平面PAC.
(Ⅲ)∵PA=AB,F是BP的中点,∴AF⊥PB,
∵PA⊥底面ABCD,BC?平面ABCD,
∴PA⊥BC,又BC⊥AB,PA?平面PAB,AB?平面PAB,PA∩AB=A,
∴BC⊥平面PAB.又∵AF?平面PAB,
∴BC⊥AF.
又∵PB⊥AF,PB?平面PBC,BC?平面PBC,PB∩BC=B,
∴AF⊥平面PBC,∵PE?平面PBC,
∴AF⊥PE.
点评 本题考查了线面平行的判定,线面垂直的性质与判定,棱锥的体积计算,属于中档题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
16.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-1,m),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则m=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
20.若函数f(x)=(k2+1)lnx-x2在区间(1,+∞)上是减函数,则实数k的取值范围是( )
| A. | [-1,1] | B. | [-$\sqrt{2}$,$\sqrt{2}$] | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-$\sqrt{2}$]∪[$\sqrt{2}$,+∞) |
14.函数f(x)=Asin(ωx+$\frac{ωπ}{2}$)(A>0,ω>0)在区间[-$\frac{3π}{4}$,-$\frac{π}{6}$]上单调递增,则ω的最大值是( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{12}{7}$ | D. | $\frac{12}{11}$ |
 正四棱柱ABCD-A1B1C1D1底面边长为$\sqrt{3}$,高为1,O为下底面的中心.
正四棱柱ABCD-A1B1C1D1底面边长为$\sqrt{3}$,高为1,O为下底面的中心.