题目内容
4．幂函数f（x）=（m2-3m+3）x${\;}^{{m^2}-2m+1}}$在区间（0，+∞）上是增函数，则m=2．分析 根据幂函数的定义求出m的值，判断即可．
解答 解：若幂函数$f（x）=（{m^2}-3m+3）{x^{{m^2}-2m+1}}$在区间（0，+∞）上是增函数，
则由m2-3m+3=1解得：m=2或m=1，
m=2时，f（x）=x，是增函数，
m=1时，f（x）=1，是常函数，
故答案为：2．
点评 本题考查了幂函数的定义，考查函数的单调性问题，是一道基础题．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
14．
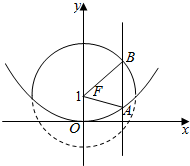如图，直线x=m与抛物线x2=4y交于点A，与圆（y-1）2+x2=4的实线部分（即在抛物线开口内的圆弧）交于点B，F为抛物线的焦点，则△ABF的周长的取值范围是（ ）
如图，直线x=m与抛物线x2=4y交于点A，与圆（y-1）2+x2=4的实线部分（即在抛物线开口内的圆弧）交于点B，F为抛物线的焦点，则△ABF的周长的取值范围是（ ）| A． | （2，4） | B． | （4，6） | C． | [2，4] | D． | [4，6] |
12．已知向量$\vec a$，$\vec b$的夹角为120°，且$|\vec a|=2$，$|\vec b|=1$，$|{\vec a+2\vec b}|$=（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{7}$ | C． | 7 | D． | 2 |
9．
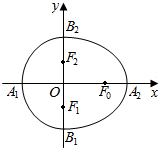我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（x＞0）与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1（x＜0）合成的曲线称作“果圆”（其中a2=b2+c2，a＞b＞c＞0）．如图，设点F0，F1，F2是相应椭圆的焦点，A1、A2和B1、B2是“果圆”与x，y轴的交点，若△F0F1F2是腰长为1的等腰直角三角形，则a，b的值分别为（ ）
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（x＞0）与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1（x＜0）合成的曲线称作“果圆”（其中a2=b2+c2，a＞b＞c＞0）．如图，设点F0，F1，F2是相应椭圆的焦点，A1、A2和B1、B2是“果圆”与x，y轴的交点，若△F0F1F2是腰长为1的等腰直角三角形，则a，b的值分别为（ ）| A． | 5，4 | B． | $\frac{{\sqrt{7}}}{2}，1$ | C． | $1，\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{6}}}{2}，1$ |
16．已知 a，b是两条不同的直线，α，β是两个不同的平面，则下列说法正确的是（ ）
| A． | 若a∥α，b∥α，则a∥b | B． | 若α⊥β，a?α，b?β，则a⊥b | ||
| C． | 若a⊥b，b⊥α，则a∥α | D． | 若α∥β，a?α，则a∥β |