题目内容
14.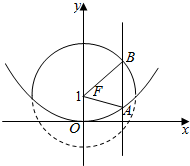 如图,直线x=m与抛物线x2=4y交于点A,与圆(y-1)2+x2=4的实线部分(即在抛物线开口内的圆弧)交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )
如图,直线x=m与抛物线x2=4y交于点A,与圆(y-1)2+x2=4的实线部分(即在抛物线开口内的圆弧)交于点B,F为抛物线的焦点,则△ABF的周长的取值范围是( )| A. | (2,4) | B. | (4,6) | C. | [2,4] | D. | [4,6] |
分析 圆(y-1)2+x2=4的圆心为(0,1),与抛物线的焦点重合,可得|FB|=2,|AF|=yA+1,|AB|=yB-yA,即可得出三角形ABF的周长=2+yA+1+yB-yA=yB+3,利用1<yB<3,即可得出.
解答 解:圆(y-1)2+x2=4的圆心为(0,1),与抛物线的焦点重合,
∴|FB|=2,|AF|=yA+1,|AB|=yB-yA,
∴三角形ABF的周长=2+yA+1+yB-yA=yB+3,
∵1<yB<3,
∴三角形ABF的周长的取值范围是(4,6).
故选:B.
点评 本题考查了抛物线与圆的标准方程及其性质、三角形的周长,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.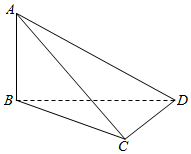 如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
 如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )| A. | 60°或90° | B. | 60° | C. | 60°或120° | D. | 30°或150° |
9.已知命题p:?x∈R,log2x=2015,则¬p为( )
| A. | ?x∉R,log2x=2015 | B. | ?x∈R,log2x≠2015 | ||
| C. | ?x0∈R,log2x0=2015 | D. | ?x0∈R,log2x0≠2015 |
6.为了得到函数y=$\sqrt{2}$sin3x的图象,可以将函数y=$\sqrt{2}$sin(3x+$\frac{π}{2}$)的图象( )
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |
3.(log227)•(log34)=( )
| A. | $\frac{1}{6}$ | B. | 2 | C. | 3 | D. | 6 |
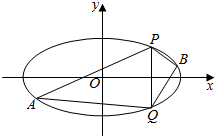 已知中心在原点,焦点在x轴上的椭圆C的离心率为$\frac{\sqrt{3}}{2}$,点(0,$\sqrt{2}$)是椭圆与y轴的一个交点.
已知中心在原点,焦点在x轴上的椭圆C的离心率为$\frac{\sqrt{3}}{2}$,点(0,$\sqrt{2}$)是椭圆与y轴的一个交点.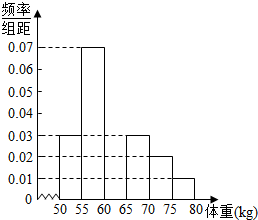 某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题:
某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题: