题目内容
13.若正方体外接球的体积是$\frac{9}{2}$π,则正方体的棱长等于$\sqrt{3}$;该正方体内切球的表面积为3π.分析 先求出正方体外接球的半径,从而求出正方体的棱长,进而求出该正方体内切球的半径,由此能求出该正方体内切球的表面积.
解答 解:设正方体外接球的半径为R,
∵正方体外接球的体积是$\frac{9}{2}$π,
∴$\frac{4}{3}π{R}^{3}$=$\frac{9}{2}π$,解得R=$\frac{3}{2}$.
设正方体的棱长为a,则$\sqrt{3}a=3$,解得a=$\sqrt{3}$,
∴该正方体内切球的半径r=$\frac{a}{2}=\frac{\sqrt{3}}{2}$,
∴该正方体内切球的表面积为S=4πr2=4π×$(\frac{\sqrt{3}}{2})^{2}$=3π.
故答案为:$\sqrt{3}$,3π.
点评 本题考查正方体的棱长及正方体内切球的表面积的求法,是中档题,注意正方体及外接球、内切球的性质的合理运用.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
3.(log227)•(log34)=( )
| A. | $\frac{1}{6}$ | B. | 2 | C. | 3 | D. | 6 |
8.从3个英语教师和5个语文教师中选取4名教师参加外事活动,其中至少要有一名英语教师,则不同的选法共有( )
| A. | $A_3^1A_5^3+A_3^2A_5^2+A_3^3A_5^1$ | |
| B. | $C_3^1C_5^3+C_3^2C_5^2+C_3^3C_5^1$ | |
| C. | $C_3^1C_7^3$ | |
| D. | $({C_3^1C_5^3+C_3^2C_5^2+C_3^3C_5^1})A_4^4$ |
18.某棱锥的三视图如图所示,则该几何体的体积为( )
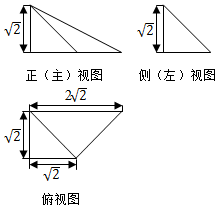

| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3$\sqrt{2}$ |
3.当x>0时,x2+mx+1≥0恒成立,且关于t的不等式t2+2t+m≤0有解,则实数m的取值范围是( )
| A. | [1,+∞) | B. | [-2,1] | C. | (-∞,-2]∪[1,+∞) | D. | (-∞,-2] |
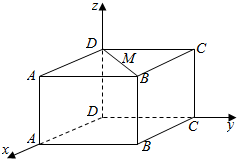 在如图所示的长方体ABCD-A1B1C1D1中,|DA|=8,|DC|=6,|DD1|=3,则D1B1的中点M的坐标为(4,3,3),|DM|=$\sqrt{34}$.
在如图所示的长方体ABCD-A1B1C1D1中,|DA|=8,|DC|=6,|DD1|=3,则D1B1的中点M的坐标为(4,3,3),|DM|=$\sqrt{34}$.