题目内容
12.已知向量$\vec a$,$\vec b$的夹角为120°,且$|\vec a|=2$,$|\vec b|=1$,$|{\vec a+2\vec b}|$=( )| A. | $\sqrt{2}$ | B. | $\sqrt{7}$ | C. | 7 | D. | 2 |
分析 利用向量的模的计算和向量的数量积公式计算即可.
解答 解:∵向量$\vec a$,$\vec b$的夹角为120°,且$|\vec a|=2$,$|\vec b|=1$,
∴$|{\vec a+2\vec b}|$2=|$\overrightarrow{a}$|2+4|$\overrightarrow{b}$|2+4$\overrightarrow{a}$•$\overrightarrow{b}$═|$\overrightarrow{a}$|2+4|$\overrightarrow{b}$|2+4|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos120°=4+4+4×2×1×(-$\frac{1}{2}$)=4,
∴$|{\vec a+2\vec b}|$=2
故选:D.
点评 本题考查了向量的模的计算和向量的数量积公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.(log227)•(log34)=( )
| A. | $\frac{1}{6}$ | B. | 2 | C. | 3 | D. | 6 |
20.已知焦点在x轴上的椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{9}$=1的离心率e=$\frac{1}{2}$,则m=( )
| A. | 12 | B. | 18 | C. | $\frac{27}{4}$ | D. | 12或$\frac{27}{4}$ |
7.不等式|x+3|+|x-1|<a2-3a有解的实数a的取值范围是( )
| A. | (-∞,-1)∪(4,+∞) | B. | (-1,4) | C. | (-∞,-4)∪(1,+∞) | D. | (-4,1) |
17.设定义在R上的偶函数y=f(x),满足对任意t∈R都有f(t)=f(2-t),且x∈[0,1]时,f(x)=-ln(x2+e),则f(2016)的值等于( )
| A. | -ln(e+1) | B. | -ln(4+e) | C. | -1 | D. | $-ln(e+\frac{1}{4})$ |
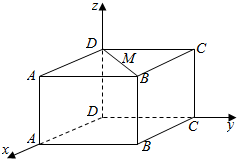 在如图所示的长方体ABCD-A1B1C1D1中,|DA|=8,|DC|=6,|DD1|=3,则D1B1的中点M的坐标为(4,3,3),|DM|=$\sqrt{34}$.
在如图所示的长方体ABCD-A1B1C1D1中,|DA|=8,|DC|=6,|DD1|=3,则D1B1的中点M的坐标为(4,3,3),|DM|=$\sqrt{34}$.