题目内容
14.已知椭圆G离心率为$\frac{\sqrt{3}}{2}$,两准线间距离为$\frac{8\sqrt{3}}{3}$,则椭圆G的标准方程为$\frac{{x}^{2}}{4}$+y2=1或$\frac{{y}^{2}}{4}$+x2=1.分析 设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1或$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),运用离心率公式和准线方程解方程可得a,c,再由a,b,c的关系,可得b,进而得到所求椭圆方程.
解答 解:设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1或$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),
则e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,$\frac{2{a}^{2}}{c}$=$\frac{8\sqrt{3}}{3}$,
解得a=2,c=$\sqrt{3}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+y2=1或$\frac{{y}^{2}}{4}$+x2=1.
故答案为:$\frac{{x}^{2}}{4}$+y2=1或$\frac{{y}^{2}}{4}$+x2=1.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和准线方程,考查运算能力,属于基础题.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
9.在△ABC中,角A,B,C的对边分别是a,b,c,面积为S,若S≥$\frac{1}{2}$ab,b2+ac=a2+c2,则a:b:c等于( )
| A. | 3:4:5 | B. | 1:1:$\sqrt{2}$ | C. | 1:$\sqrt{2}$:$\sqrt{3}$ | D. | 1:$\sqrt{3}$:2 |
3.当x>0时,x2+mx+1≥0恒成立,且关于t的不等式t2+2t+m≤0有解,则实数m的取值范围是( )
| A. | [1,+∞) | B. | [-2,1] | C. | (-∞,-2]∪[1,+∞) | D. | (-∞,-2] |
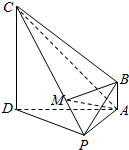 在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).
在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1). 如图所示,在四棱锥A-BCDE中,AE⊥平面BCDE.△BCE是正三角形,BD和CE的交点恰好平分CE,又AE=BE=2,∠CDE=120°,AG=$\frac{\sqrt{2}}{2}$.
如图所示,在四棱锥A-BCDE中,AE⊥平面BCDE.△BCE是正三角形,BD和CE的交点恰好平分CE,又AE=BE=2,∠CDE=120°,AG=$\frac{\sqrt{2}}{2}$.