题目内容

函数f（x）=x3+bx2+cx是奇函数，函数g（x）=x2+（c-2）x+5是偶函数，则b+c=
 
．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：由f（x）=x3+bx2+cx是奇函数，则有f（-x）=-f（x），可得b．由g（x）=x2 +（c-2）x+5是偶函数，故有g（-x）=g（x），可得c．
解答： 解：若f（x）=x3+bx2+cx是奇函数，则有f（-x）=f（x），即 （-x）3+bx2-cx=-（x3+bx2+cx），∴b=0．
由g（x）=x2 +（c-2）x+5是偶函数，故有g（-x）=g（x），故（-x）2 -（c-2）x+5是x2 +（c-2）x+5，∴c=2，
∴b+c=2．
故答案为：2．
点评：本题主要考查奇偶函数的定义．函数的奇偶性的判断，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=|xex|，方程f2（x）+tf（x）+1=0（t∈R）有四个不同的实数根，则t的取值范围为（　　）
A、（-∞，-
e2+1
e
）
B、（-∞，-2）
C、（-
e2+1
e
，-2）
D、（
e2+1
e
，+∞）
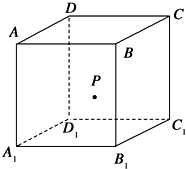如图正方体A1B1C1D1-ABCD的侧面AB1内有动点P到直线AB与到直线B1C1的距离相等，则动点P所在的曲线的形状为 （　　）
A、
B、
C、
D、
已知等差数列{an}的前六项的和为60，且a1=5．
（1）求数列{an}的通项公式an及前n项和Sn；
（2）若数列{bn}满足bn+1-bn=an（n∈N*），b1=3，求数列{
1
bn
}的前n项和Tn．
已知平面向量
a
=（-1，1），
b
=（4，1），若|λ
a
+
b
|=
13
，则实数λ=
 
．
使（3-2x-x2） -
1
4
有意义的x的取值范围是
 
．
定义在（-1，1）上的函数f（x）-f（y）=f（
x-y
1-xy
），当x∈（-1，0）时f（x）＞0．若P=f（
1
5
）+f（
1
11
），Q=f（
1
2
），R=f（0），则P，Q，R的大小关系为
 
．
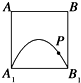
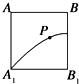
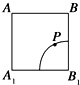
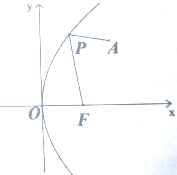如图，F是抛物线C：y2=2px的焦点，点A（4，2）为抛物线于内一点，点P为抛物线上一动点，|PA|+|PF|的最小值为8
（1）求抛物线方程；
（2）在抛物线内过点F任意作互相垂直的两条弦MN和RS，问是否存在定点Q，使过点Q的动直线同时平分这两条弦，若存在，求出定点Q的坐标；若不存在，请说明理由．
已知不等式-2xy≤ax2+2y2，若对任意x∈[1，2]及y∈[-1，3]不等式恒成立，则实数a的范围是（　　）
A、0≤a≤
1
2
B、a≥0
C、a≥
1
2
D、a≥-
15
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网