题目内容
3.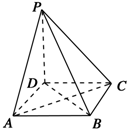 如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a,
如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a,(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
(3)若E是PC的中点,求二面角E-BD-C的正切值.
分析 (1)由勾股定理得:PD⊥DC,PD⊥AD,再由线面垂直的判定定理,可得PD⊥平面ABCD;
(2)由(1)知PD⊥平面ABCD,结合底面是边长为a的正方形,可得AC⊥平面PDB,再由面面垂直的判定定理,可得:平面PAC⊥平面PBD;
(3)过点E作EF⊥CD于F,过F作HF⊥BD于H,故∠FHE为二面角E-BD-C的平面角,解得:二面角E-BD-C的正切值.
解答 证明:(1)∵PD=a,DC=a,PC=$\sqrt{2}$a,
∴PC2=PD2+DC2,
∴PD⊥DC.
同理可证PD⊥AD,又AD∩DC=D,
∴PD⊥平面ABCD.
(2)由(1)知PD⊥平面ABCD,
∴PD⊥AC,而四边形ABCD是正方形,
∴AC⊥BD,又BD∩PD=D,
∴AC⊥平面PDB.
同时,AC?平面PAC,
∴平面PAC⊥平面PBD.
(3)过点E作EF⊥CD于F,过F作HF⊥BD于H,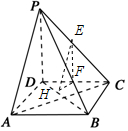
故∠FHE为二面角E-BD-C的平面角.
在Rt△EFH中,tan∠FHE=$\sqrt{2}$.
点评 本题考查的知识点是线面垂直的判定,面面垂直的判定,二面角的平面角及求解,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列说法正确的是( )
| A. | 函数y=|x|有极大值,但无极小值 | B. | 函数y=|x|有极小值,但无极大值 | ||
| C. | 函数y=|x|既有极大值又有极小值 | D. | 函数y=|x|无极值 |
11.已知函数f(x)=xln x,g(x)=(-x2+ax-3)ex(a为实数).
(1)当a=5时,求函数y=g(x)在x=1处的切线方程;
(2)求f(x)在区间[t,t+2](t>0)上的最小值.
(1)当a=5时,求函数y=g(x)在x=1处的切线方程;
(2)求f(x)在区间[t,t+2](t>0)上的最小值.
8.若一个正三棱锥的正(主)视图如图所示,则其体积等于( )
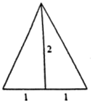

| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
15.已知点A(4,8)是抛物线C:y2=2px与直线l:y=k(x+4)的一个交点,则抛物线的焦点到直线l的距离是( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |