题目内容
13.设函数f(x)=2cos2x+$\sqrt{3}$sin2x.(1)求函数f(x)的最小正周期和单调递增区间;
(2)求函数f(x)的最小值及x的取值集合.
分析 (1)利用二倍角公式以及两角和与差的三角函数化简函数的解析式,然后求解函数的周期,利用正弦函数的单调性求解单调增区间即可.
(2)利用正弦函数的最值求解函数的最值即可.
解答 解:(1)∵$f(x)=2{cos^2}x+\sqrt{3}sin2x=2sin({2x+\frac{π}{6}})+1$….(2分)
∴$函数f(x)的最小正周期T=\frac{2π}{2}=π$….(3分)
由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,
kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,k∈Z
所以函数的单调递增区间是$[{kπ-\frac{π}{3},kπ+\frac{π}{6}}](k∈Z)$…(6分).
(2)函数f(x)=2cos2x+$\sqrt{3}$sin2x=2sin(2x+$\frac{π}{6}$)+1≥-2+1=-1.
函数的最小值为:-1.…8分
当且仅当2x+$\frac{π}{6}$=2kπ$-\frac{π}{2}$,k∈Z时取最小值.
即x=kπ$-\frac{π}{3}$,k∈Z.…10分.
点评 本题考查两角和与差的三角函数,函数的周期的求法,函数的单调性,三角函数的最值的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
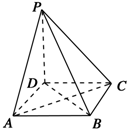 如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a,
如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a,