题目内容
11.已知函数f(x)=xln x,g(x)=(-x2+ax-3)ex(a为实数).(1)当a=5时,求函数y=g(x)在x=1处的切线方程;
(2)求f(x)在区间[t,t+2](t>0)上的最小值.
分析 (1)求出切点坐标,函数的导数,求出切线的斜率,然后求解切线方程.
(2)求出函数的定义域,函数的导数,通过导函数的符号,判断函数的单调性,然后求解函数的最值.
解答 解:(1)当a=5时,
g(x)=(-x2+5x-3)ex,g(1)=e.
又g′(x)=(-x2+3x+2)ex,故切线的斜率为g′(1)=4e.
所以切线方程为:y-e=4e(x-1),即y=4ex-3e.
(2)函数f(x)的定义域为(0,+∞),f′(x)=ln x+1,
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (0,$\frac{1}{e}$) | $\frac{1}{e}$ | ($\frac{1}{e}$,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 单调递减 | 极小值 | 单调递增 |
②当0<t<$\frac{1}{e}$时,在区间[t,$\frac{1}{e}$)上f(x)为减函数,在区间$(\frac{1}{e},t+2]$上f(x)为增函数,
所以f(x)min=f($\frac{1}{e}$)=-$\frac{1}{e}$.
点评 本题考查函数的导数的应用,切线方程,以及函数的最值的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
20.设M为△ABC内一点,且$\overrightarrow{AM}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AC}$,则△ABM与△ABC的面积之比为( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
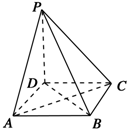 如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a,
如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a,