题目内容
18．已知函数f（x）=$\frac{1}{x}$+alnx（a≠0，a∈R）．（1）若a=1，求函数f（x）的极值和单调区间；
（2）若在区间（0，e]上至少存在一点x0，使得f（x0）＜0成立，求实数a的取值范围．
分析 （1）求函数f（x）的导数，令导数等于零，解方程，再求出函数f（x）的导数和驻点，然后列表讨论，求函数f（x）的单调区间和极值；
（2）若在区间（0，e]上存在一点x0，使得f（x0）＜0成立，其充要条件是f（x）在区间（0，e]上的最小值小于0即可．利用导数研究函数在闭区（0，e]上的最小值，先求出导函数f'（x），然后讨论研究函数在（0，e]上的单调性，将f（x）的各极值与其端点的函数值比较，其中最小的一个就是最小值．
解答 解：（1）因为f′（x）=-$\frac{1}{{x}^{2}}$+$\frac{a}{x}$=$\frac{ax-1}{{x}^{2}}$，（2分）
当a=1，f′（x）=$\frac{x-1}{{x}^{2}}$，
令f'（x）=0，得x=1，（3分）
又f（x）的定义域为（0，+∞），f'（x），f（x）随x的变化情况如下表：
| x | （0，1） | 1 | （1，+∞） |
| f'（x） | - | 0 | + |
| f（x） | ↘ | 极小值 | ↗ |
f（x）的单调递增区间为（1，+∞），单调递减区间为（0，1）；（6分
（2）∵f′（x）=$\frac{ax-1}{{x}^{2}}$，（a≠0，a∈R）．
令f′（x）=0，得到x=$\frac{1}{a}$，
若在区间[0，e]上存在一点x0，使得f（x0）＜0成立，
其充要条件是f（x）在区间（0，e]上的最小值小于0即可．
（i）当x=$\frac{1}{a}$＜0，即a＜0时，f′（x）＜0对x∈（0，+∞）成立，
∴f（x）在区间（0，e]上单调递减，
故f（x）在区间（0，e]上的最小值为f（e）=$\frac{1}{e}$+alne=$\frac{1}{e}$+a，
由$\frac{1}{e}$+a＜0，得a＜-$\frac{1}{e}$；
（ii）当x=$\frac{1}{a}$＞0，即a＞0时，
①若e≤$\frac{1}{a}$，则f′（x）≤0对x∈（0，e]成立，
∴f（x）在区间（0，e]上单调递减，
∴f（x）在区间（0，e]上的最小值为f（e）=$\frac{1}{e}$+alne=$\frac{1}{e}$+a＞0，
显然，f（x）在区间（0，e]上的最小值小于0不成立．
②若1＜$\frac{1}{a}$＜e，即a＞$\frac{1}{e}$时，则有
| x | （0，$\frac{1}{a}$） | $\frac{1}{a}$ | （$\frac{1}{a}$，e） |
| f′（x） | - | 0 | + |
| f（x） | ↘ | 极小值 | ↗ |
由f（$\frac{1}{a}$）=a+aln$\frac{1}{a}$=a（1-lna）＜0，
得1-lna＜0，解得a＞e，即a∈（e，+∞）．
综上，由（1）（2）可知：a∈（-∞，-$\frac{1}{e}$）∪（e，+∞）．
点评 本题主要考查导数的几何意义以及利用导数求函数的最值问题，考查学生的计算能力，综合性较强，运算量较大，有一定的难度．
练习册系列答案
相关题目
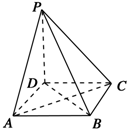如图所示，在四棱锥P-ABCD中，底面是边长为a的正方形，侧棱PD=a，PA=PC=$\sqrt{2}$a，
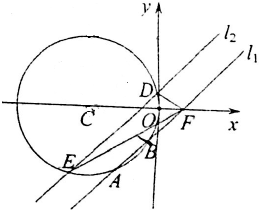已知直线l1：y=x-1与圆C：（x+a）2+y2=a2（a＞0）相交于A、B两点，|AB|=2，直线l2∥l1，直线l2与圆C相交于D、E两点．