题目内容
定义:满足对任意的正整数n,an+2-an+1≤an+1-an都成立的数列{an}为“降步数列”.给出以下数列{an}(n∈N*):
①an=5n+3;②an=n2+n+1;③an=
;④an=2n+
;⑤an=
;
其中是“降步数列”的有 (写出所有满足条件的序号)
①an=5n+3;②an=n2+n+1;③an=
| n |
| 1 |
| n |
| 1 |
| n2+n |
其中是“降步数列”的有
考点:数列的应用
专题:等差数列与等比数列
分析:对所给的五个数列,利用“降步数列”的概念,逐个进行验证,能求出结果.
解答:
解:在①中,∵an=5n+3,
∴an+2-an+1=5(n+2)-5(n+1)=5,
an+1-an=5(n+1)-5n=5,
∴对任意的正整数n,an+2-an+1≤an+1-an都成立,故①是“降步数列”;
在②中,∵an=n2+n+1,
∴an+2-an+1=(n+2)2+(n+2)+1-[(n+1)2+(n+1)+1]=2n+4,
an+1-an=(n+1)2+(n+1)+1-(n2+n+1)=2n+2,
∴对任意的正整数n,an+2-an+1>an+1-an都成立,故②不是“降步数列”;
在③中,∵an=
,
∴an+2-an+1=
-
,
an+1-an=
-
,
∴对任意的正整数n,an+2-an+1≤an+1-an都成立,故③是“降步数列”;
在④中,∵an=2n+
,
∴an+2-an+1=2(n+2)+
-[2(n+1)+
]=2+
-
,
an+1-an=2(n+1)+
-2n-
=2+
-
,
∴当n=1时,an+2-an+1>an+1-an成立,故④不是“降步数列”;
在⑤中,∵an=
,
∴a3-a2=
-
=-
,
a2-a1=
-
=-
,
∴当n=1时,an+2-an+1>an+1-an成立,故⑤不是“降步数列”.
故答案为:①③.
∴an+2-an+1=5(n+2)-5(n+1)=5,
an+1-an=5(n+1)-5n=5,
∴对任意的正整数n,an+2-an+1≤an+1-an都成立,故①是“降步数列”;
在②中,∵an=n2+n+1,
∴an+2-an+1=(n+2)2+(n+2)+1-[(n+1)2+(n+1)+1]=2n+4,
an+1-an=(n+1)2+(n+1)+1-(n2+n+1)=2n+2,
∴对任意的正整数n,an+2-an+1>an+1-an都成立,故②不是“降步数列”;
在③中,∵an=
| n |
∴an+2-an+1=
| n+2 |
| n+1 |
an+1-an=
| n+1 |
| n |
∴对任意的正整数n,an+2-an+1≤an+1-an都成立,故③是“降步数列”;
在④中,∵an=2n+
| 1 |
| n |
∴an+2-an+1=2(n+2)+
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+1 |
an+1-an=2(n+1)+
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n |
∴当n=1时,an+2-an+1>an+1-an成立,故④不是“降步数列”;
在⑤中,∵an=
| 1 |
| n2+n |
∴a3-a2=
| 1 |
| 12 |
| 1 |
| 6 |
| 1 |
| 12 |
a2-a1=
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
∴当n=1时,an+2-an+1>an+1-an成立,故⑤不是“降步数列”.
故答案为:①③.
点评:本题考查“降步数列”的判断,是中档题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列赋值语句中正确的是( )
| A、m+n=3 | B、3=i |
| C、i=i+1 | D、i=j=3 |
 如图,空间四边形ABCD中,P、Q、R分别是AB、AD、CD的中点,平面PQR交BC于点S.
如图,空间四边形ABCD中,P、Q、R分别是AB、AD、CD的中点,平面PQR交BC于点S.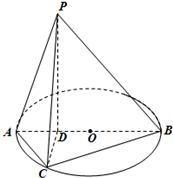 如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.
如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=PD=3,AC=2AD=2.