题目内容
已知数列{an}和{bn},其中a1=1,且数列{an}的相邻两项an、an+1是关于x的方程x2-2nx+bn=0(n∈N*)的两个实根.
(1)求证:数列{an-
×2n}是等比数列;
(2)求数列{an}和{bn}的通项公式;
(3)设Sn为数列{an}的前n项和,问是否存在常数λ,使得bn>λSn对任意的n∈N都成立?若存在,求出λ的取值范围;若不存在,请说明理由.
(1)求证:数列{an-
| 1 |
| 3 |
(2)求数列{an}和{bn}的通项公式;
(3)设Sn为数列{an}的前n项和,问是否存在常数λ,使得bn>λSn对任意的n∈N都成立?若存在,求出λ的取值范围;若不存在,请说明理由.
考点:数列的求和,等比关系的确定,数列递推式
专题:等差数列与等比数列
分析:(1)利用定义法证明只需
为常数即可.
(2)根据(1)的结论进一步求出数列{an}和{bn}的通项公式.
(3)由于(1)和(2)的通项已求出,直接对n进行分类讨论,利用恒成立问题求出结论.
an+1-
| ||
an-
|
(2)根据(1)的结论进一步求出数列{an}和{bn}的通项公式.
(3)由于(1)和(2)的通项已求出,直接对n进行分类讨论,利用恒成立问题求出结论.
解答:
(1)证明:数列{an}的相邻两项an、an+1是关于x的方程x2-2nx+bn=0(n∈N*)的两个实根.
则:
所以:
=
=-1(常数),
其中a1=1,a1-
=
故数列{an-
•2n}是以
为首项,公比为-1的等比数列.
(2)解:由于数列{an}是等比数列
所以:an-
•2n=
•(-1)n-1
解得:an=
[2n-(-1)n-1]
Sn=a1+a2+…+an=
[(2+22+…+2n-(-1)-(-1)2-…-(-1)n]
=
(2n+1-2-
)
所以:bn=anan+1=
(22n+1-(-2)n-1)
(3)假设存在实数λ使得bn>λSn对任意的n∈N都成立,
则:只需满足
(2n+1-1)(2n+1)>
(2n+1-2-
)即可.
①当n为正奇数时,
(2n+1-1)(2n+1)-
(2n+1-1)>0
由于2n+1-1>0,
所以:λ<
(2n+1)对任意的正奇数都成立.
则:当n=1时,
(2n+1)=1
则:λ<1.
②当n为正偶数时,
(2n+1-1)(2n+1)-
(2n-1)>0
由于2n-1>0
则:λ<
(2n+1+1)对任意的正偶数都成立.
所以:
(2n+1+1)的最小值为
.
所以:λ<
.
由①②得:λ<1
故存在实数λ,使得bn>λSn对任意的n∈N都成立,λ的范围为:(-∞,1).
则:
|
所以:
an+1-
| ||
an-
|
2n-an-
| ||
an-
|
其中a1=1,a1-
| 2 |
| 3 |
| 1 |
| 3 |
故数列{an-
| 1 |
| 3 |
| 1 |
| 3 |
(2)解:由于数列{an}是等比数列
所以:an-
| 1 |
| 3 |
| 1 |
| 3 |
解得:an=
| 1 |
| 3 |
Sn=a1+a2+…+an=
| 1 |
| 3 |
=
| 1 |
| 3 |
| (-1)n-1 |
| 2 |
所以:bn=anan+1=
| 1 |
| 9 |
(3)假设存在实数λ使得bn>λSn对任意的n∈N都成立,
则:只需满足
| 1 |
| 9 |
| λ |
| 3 |
| (-1)n-1 |
| 2 |
①当n为正奇数时,
| 1 |
| 9 |
| λ |
| 3 |
由于2n+1-1>0,
所以:λ<
| 1 |
| 3 |
则:当n=1时,
| 1 |
| 3 |
则:λ<1.
②当n为正偶数时,
| 1 |
| 9 |
| 2λ |
| 3 |
由于2n-1>0
则:λ<
| 1 |
| 6 |
所以:
| 1 |
| 6 |
| 3 |
| 2 |
所以:λ<
| 3 |
| 2 |
由①②得:λ<1
故存在实数λ,使得bn>λSn对任意的n∈N都成立,λ的范围为:(-∞,1).
点评:本题考查的知识要点:数列的求和,数列通项公式的求法,恒成立问题的应用,分类讨论思想的应用,及相关的运算问题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
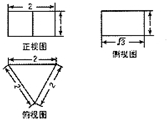
一个几何体的三视图如图所示,则这个几何体的体积为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、2
|