题目内容
已知函数f(α)=2sin(α+
),其中角α的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤α≤π.若点P(x,y)为平面区域
上的一个动点,则f(α)的取值范围是 .
| π |
| 4 |
|
考点:函数y=Asin(ωx+φ)的图象变换,简单线性规划
专题:三角函数的图像与性质
分析:作出不等式组对应的平面区域,利用数形结合求出角α的范围,利用三角函数的图象和性质即可得到结论.
解答:
解: 作出不等式组对应的平面区域如图:
作出不等式组对应的平面区域如图:
由图象可知当点P位于线段AB上时,此时角α最小,值为
,
点P位于C时,此时角α最大为
,
即
≤α≤
,
则
+
≤α+
≤
+
,
即
≤α+
≤
,
∴2×
≤2sin(α+
)≤2,
即
≤2sin(α+
)≤2,
∴f(α)的取值范围是[
,2]
故答案为:[
,2]
 作出不等式组对应的平面区域如图:
作出不等式组对应的平面区域如图:由图象可知当点P位于线段AB上时,此时角α最小,值为
| π |
| 4 |
点P位于C时,此时角α最大为
| π |
| 2 |
即
| π |
| 4 |
| π |
| 2 |
则
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
即
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
∴2×
| ||
| 2 |
| π |
| 4 |
即
| 2 |
| π |
| 4 |
∴f(α)的取值范围是[
| 2 |
故答案为:[
| 2 |
点评:本题主要考查三角函数的图象和性质,利用线性规划的知识求出角α的范围是解决本题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
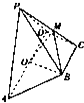 如图四棱锥P-ABCD的底面是一等腰梯形,其中AD∥BC,其中AD=3BC=6,AB=DC=2
如图四棱锥P-ABCD的底面是一等腰梯形,其中AD∥BC,其中AD=3BC=6,AB=DC=2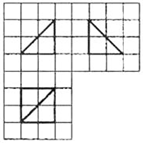 如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体外接球的体积为
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体外接球的体积为