题目内容
已知a+b+c>0,ab+bc+ca>0且abc>0,求证:a、b、c都大于零.用反证法证明时,应先假设 .
考点:反证法与放缩法
专题:证明题,反证法
分析:用反证法证明某命题时,应先假设命题的否定成立,而命题的否定为:“a、b、c不都大于零”,由此得出结论.
解答:
解:用反证法证明某命题时,应先假设命题的否定成立,
而:“a、b、c都大于零”的否定为:“a、b、c不都大于零”.
故答案为:a、b、c不都大于零.
而:“a、b、c都大于零”的否定为:“a、b、c不都大于零”.
故答案为:a、b、c不都大于零.
点评:本题主要考查用反证法证明数学命题,把要证的结论进行否定,得到要证的结论的反面,是解题的关键.

练习册系列答案
相关题目
若P(A)=
,P(B|A)=
,则P(AB)等于( )
| 9 |
| 10 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2014,则i+j=
把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2014,则i+j=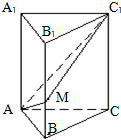 如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=
如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=