题目内容
14.下列命题中真命题是( )| A. | 若m⊥α,m?β,则α⊥β | |
| B. | 若m?α,n?α,m∥β,n∥β,则α∥β | |
| C. | 若m?α,n?α,m,n是异面直线,那么n与α相交 | |
| D. | 若α∩β=m,n∥m,则n∥α且n∥β |
分析 A.根据面面垂直的判定定理进行判断
B.根据面面平行的判定定理进行判断
C.根据直线和平面的位置关系进行判断
D.根据线面平行的性质进行判断.
解答 解:A.若m⊥α,m?β,则α⊥β成立,
B.若m?α,n?α,m∥β,n∥β,当α与β相交时,满足α∥β,当α与β不相交时,结论不成立,
C.若m?α,n?α,m,n是异面直线,那么n与α相交,或n∥α,故C错误,
D.若α∩β=m,n∥m,则n∥α且n∥β错误,有可能n?α或n?β,故D错误,
故选:A
点评 本题主要考查命题的真假判断,涉及空间直线和平面平行或垂直的判定,根据相应的定理是解决本题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
5.由0,1,2,…,9这10个数字组成的无重复数字的四位数中,个位数字与十位数字之差的绝对值等于8的数有( )
| A. | 180个 | B. | 196个 | C. | 210个 | D. | 224个 |
9.已知实数x,y满足-1≤x+y≤2,3≤4x+y≤4,则9x+y的取值范围是( )
| A. | [$\frac{14}{3}$,$\frac{37}{3}$] | B. | [$\frac{1}{3}$,$\frac{50}{3}$] | C. | [$\frac{11}{3}$,6] | D. | [$\frac{41}{6}$,$\frac{22}{3}$] |
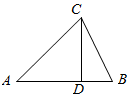 如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$
如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$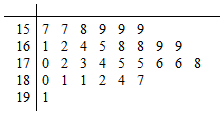 为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”
为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”