题目内容
19．
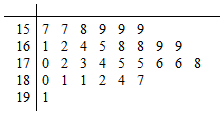为了解某种树苗培育情况，研究所在苗圃基地花木园中随机抽出30株树苗的主体高，编成如图所示的茎叶图，若苗主体高在169cm以上（包括169cm）定义为“优质苗”，高在169cm以下（不包括169cm）定义为“普苗”（1）如果用分层抽样的方法从“优质苗”和“普苗”中抽取5株，再从这5株中选2株，那么至少有1株是“优质苗”的概率是多少？
（2）根据统计学的基本思想，用样本估计总体，把频率作为概率，若从该花木园随机选3株出售，价格是：“优质苗”每株3，“普苗”每株1（单位：千元）用X表示销售3株的总收入，试写出X的分布列，并求X的数学期望．
分析 （1）由茎叶图得用分层抽样的方法从“优质苗”和“普苗”中抽取5株，抽到株“优质苗”，抽到2株“普苗”，再从这5株中选2株，求出基本基本总数，利用对立事件概率计算公式能求出至少有1株是“优质苗”的概率．
（2）由已知得X的可能能取值为3，5，7，9，分别求出相应的概率，由此能求出X的分布列和EX．
解答 解：（1）由茎叶图得“优质苗”有18株，“普苗”有12株，
用分层抽样的方法从“优质苗”和“普苗”中抽取5株，
抽到$\frac{5}{30}×18$=3株“优质苗”，抽到$\frac{5}{30}×12$=2株“普苗”，
再从这5株中选2株，基本基本总数n=${C}_{5}^{2}$=10，
至少有1株是“优质苗”的概率：p=1-$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{9}{10}$．
∴至少有1株是“优质苗”的概率是$\frac{9}{10}$．
（2）由已知得X的可能能取值为3，5，7，9，
P（X=3）=$\frac{{C}_{12}^{3}}{{C}_{30}^{3}}$=$\frac{220}{4060}$=$\frac{55}{1015}$，
P（X=5）=$\frac{{C}_{12}^{2}{C}_{18}^{1}}{{C}_{30}^{3}}$=$\frac{1188}{4060}$=$\frac{297}{1015}$，
P（X=7）=$\frac{{C}_{12}^{1}{C}_{18}^{2}}{{C}_{30}^{3}}$=$\frac{1836}{4060}$=$\frac{459}{1015}$，
P（X=9）=$\frac{{C}_{18}^{3}}{{C}_{30}^{3}}$=$\frac{816}{4060}$=$\frac{204}{1015}$，
∴X的分布列为：
| X | 3 | 5 | 7 | 9 |
| P | $\frac{55}{1015}$ | $\frac{297}{1015}$ | $\frac{459}{1015}$ | $\frac{204}{1015}$ |
点评 本题考查概率的求法，考查离散型随机变量的分布列的求法，是中档题，解题时要认真审题，注意茎叶图、分层抽样的性质的合理运用．
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
| A． | [-$\frac{1}{8}$，1] | B． | [0，1] | C． | [0，$\frac{1}{4}$] | D． | [-$\frac{1}{9}$，1] |
| 选手年龄 | [5，15） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） |
| 频数 | 2 | 12 | 16 | 10 | 7 | 3 |
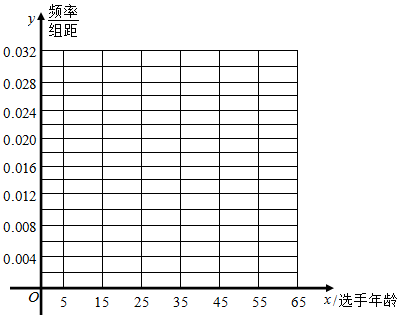
（Ⅱ）若将频率视为概率，从参与节目的选手中随机抽取3位（看作有放回地抽取），求年龄在[35，45）内的选手人数X的分布列、数学期望．
| A． | 若m⊥α，m?β，则α⊥β | |
| B． | 若m?α，n?α，m∥β，n∥β，则α∥β | |
| C． | 若m?α，n?α，m，n是异面直线，那么n与α相交 | |
| D． | 若α∩β=m，n∥m，则n∥α且n∥β |
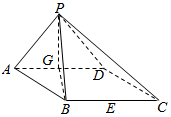如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，且∠DAB=60°，侧面PAD为正三角形，其所在平面垂直于底面ABCD，G为AD边的中点，E为BC所在直线上的一点