题目内容
若x，y∈R+，x+4y=20，则xy的最大值为（ ）
| A、20 | B、100 | C、64 | D、25 |
考点：基本不等式
专题：不等式的解法及应用
分析：由题意可得xy=
•x•4y≤
（
）2=25，验证等号成立的条件即可．
| 1 |
| 4 |
| 1 |
| 4 |
| x+4y |
| 2 |
解答：
解：∵x，y∈R+，x+4y=20，
∴xy=
•x•4y≤
（
）2=25
当且仅当x=4y即x=10且y=
时取等号，
故选：D
∴xy=
| 1 |
| 4 |
| 1 |
| 4 |
| x+4y |
| 2 |
当且仅当x=4y即x=10且y=
| 5 |
| 2 |
故选：D
点评：本题考查基本不等式求最值，属基础题．
练习册系列答案
相关题目
“x＜0”是“log2（x+1）＜0”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也必要条件 |
若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（ ）
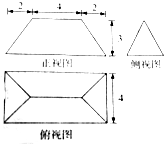
| A、24cm3 |
| B、40cm3 |
| C、36cm3 |
| D、48cm3 |
设a=40.1，b=log30.1，c=0.50.1，则（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞a＞c |
| D、b＞c＞a |