题目内容
已知函数f(x)=
x3-2ax2-3x(a∈R)
(1)若函数y=f(x)在(-1,1)内是减函数,求a的取值范围
(2)若函数y=f(x)在(-1,1)内有且只有一个极值点,求a的取值范围.
| 2 |
| 3 |
(1)若函数y=f(x)在(-1,1)内是减函数,求a的取值范围
(2)若函数y=f(x)在(-1,1)内有且只有一个极值点,求a的取值范围.
考点:函数单调性的判断与证明,利用导数研究函数的极值
专题:函数的性质及应用,导数的综合应用
分析:(1)先求f′(x)=2x2-4ax-3,所以若函数y=f(x)在(-1,1)内是减函数,则f′(x)≤0在(-1,1)内恒成立,所以
,解不等式组即得a的取值范围;
(2)令f′(x)=0,容易判断该方程在R上有两个不同实根,而若函数y=f(x)在(-1,1)内有且只有一个极值点,则该方程在(-1,1)内只有一个解,所以得到f′(-1)•f′(1)<0,解不等式即得a的取值范围.
|
(2)令f′(x)=0,容易判断该方程在R上有两个不同实根,而若函数y=f(x)在(-1,1)内有且只有一个极值点,则该方程在(-1,1)内只有一个解,所以得到f′(-1)•f′(1)<0,解不等式即得a的取值范围.
解答:
解:(1)f'(x)=2x2-4ax-3≤0在(-1,1)内恒成立;
∴
,即
;
解得-
≤a≤
;
∴a的取值范围为[-
,
];
(2)令f'(x)=2x2-4ax-3=0;
∵△=16a2+24>0;
∴该方程有两个不同实根;
若函数y=f(x)在(-1,1)内有且只有一个极值点,则该方程在(-1,1)内只有一个解;
∴f'(-1)•f'(1)<0,即1-16a2<0,解得:
a<-
或a>
;
∴a的取值范围为(-∞,-
)∪(
,+∞).
∴
|
|
解得-
| 1 |
| 4 |
| 1 |
| 4 |
∴a的取值范围为[-
| 1 |
| 4 |
| 1 |
| 4 |
(2)令f'(x)=2x2-4ax-3=0;
∵△=16a2+24>0;
∴该方程有两个不同实根;
若函数y=f(x)在(-1,1)内有且只有一个极值点,则该方程在(-1,1)内只有一个解;
∴f'(-1)•f'(1)<0,即1-16a2<0,解得:
a<-
| 1 |
| 4 |
| 1 |
| 4 |
∴a的取值范围为(-∞,-
| 1 |
| 4 |
| 1 |
| 4 |
点评:考查函数单调性和函数导数符号的关系,以及对二次函数图象的掌握,函数极值的概念,函数在极值点处导数的取值情况.

练习册系列答案
相关题目
设x,y满足约束条件
,则x+2y+3的取值范围是( )
|
| A、[1,5] |
| B、[2,6] |
| C、[3,10] |
| D、[3,11] |
已知点A(1,3),B(-2,-1).若直线l:y=k(x-2)+1与线段AB相交,则k的取值范围是( )
A、[
| ||
| B、(-∞,-2] | ||
C、(-∞,-2]∪[
| ||
D、[-2,
|
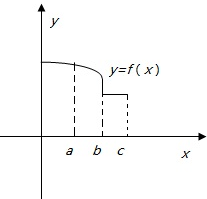 函数y=f(x)的图象如图所示,试画出导函数f′(x)的大致形状.
函数y=f(x)的图象如图所示,试画出导函数f′(x)的大致形状.