题目内容
已知点A(1,3),B(-2,-1).若直线l:y=k(x-2)+1与线段AB相交,则k的取值范围是( )
A、[
| ||
| B、(-∞,-2] | ||
C、(-∞,-2]∪[
| ||
D、[-2,
|
考点:直线的斜率
专题:直线与圆
分析:由直线系方程求出直线l所过定点,由两点求斜率公式求得连接定点与线段AB上点的斜率的最小值和最大值得答案.
解答:
解:∵直线l:y=k(x-2)+1过点P(2,1),
连接P与线段AB上的点A(1,3)时直线l的斜率最小,为kPA=
=-2,
连接P与线段AB上的点B(-2,-1)时直线l的斜率最大,为kPB=
=
.
∴k的取值范围是[-2,
].
故选:D.
连接P与线段AB上的点A(1,3)时直线l的斜率最小,为kPA=
| 1-3 |
| 2-1 |
连接P与线段AB上的点B(-2,-1)时直线l的斜率最大,为kPB=
| -1-1 |
| -2-2 |
| 1 |
| 2 |
∴k的取值范围是[-2,
| 1 |
| 2 |
故选:D.
点评:本题考查了直线的斜率,考查了直线系方程,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}是等比数列,其前n项和为Sn,若a4=4a3,S4=1,则S8=( )
| A、257 | B、16 |
| C、15 | D、256 |
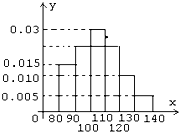 某校高一某班共有64名学生,如图是该班某次数学考试成绩的频率分布直方图,根据该图可知,成绩在110-120间的同学大约有( )
某校高一某班共有64名学生,如图是该班某次数学考试成绩的频率分布直方图,根据该图可知,成绩在110-120间的同学大约有( )| A、10 | B、11 | C、13 | D、16 |