题目内容
设x,y满足约束条件
,则x+2y+3的取值范围是( )
|
| A、[1,5] |
| B、[2,6] |
| C、[3,10] |
| D、[3,11] |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最值.
解答:
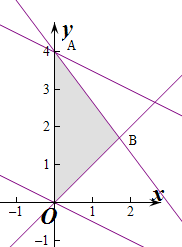 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
设z=x+2y+3得y=-
x+
z-
,
平移直线y=-
x+
z-
,aaa
由图象可知当直线y=-
x+
z-
经过点A(0,4)时,直线y=-
x+
z-
的截距最大,
此时z最大.为z=8+3=11,
当直线y=-
x+
z-
经过点O(0,4)时,直线y=-
x+
z-
的截距最小,
此时z最小为z=3,
故3≤z≤11
故选:D
 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).设z=x+2y+3得y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
平移直线y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
由图象可知当直线y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
此时z最大.为z=8+3=11,
当直线y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
此时z最小为z=3,
故3≤z≤11
故选:D
点评:本题主要考查线性规划的应用,利用图象平行求得目标函数的最大值和最小值,利用数形结合是解决线性规划问题中的基本方法.

练习册系列答案
相关题目
下列命题中,假命题为( )
| A、存在四边相等的四边形不是正方形 |
| B、z1,z2∈C,z1+z2为实数的充分必要条件是z1,z2为共轭复数 |
| C、若x,y∈R,且x+y>2则x,y至少有一个大于1 |
| D、命题:?n∈N,2n>1000的否定是:?n∈N,2n≤1000 |
二项式(3x-
)7展开式中,含x-3项的系数是( )
| 1 | |||
|
| A、-12 | B、18 |
| C、-20 | D、21 |
已知数列{an}是等比数列,其前n项和为Sn,若a4=4a3,S4=1,则S8=( )
| A、257 | B、16 |
| C、15 | D、256 |
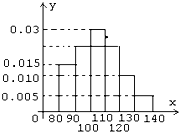 某校高一某班共有64名学生,如图是该班某次数学考试成绩的频率分布直方图,根据该图可知,成绩在110-120间的同学大约有( )
某校高一某班共有64名学生,如图是该班某次数学考试成绩的频率分布直方图,根据该图可知,成绩在110-120间的同学大约有( )| A、10 | B、11 | C、13 | D、16 |