题目内容
如图，四边形ABCD、BCFE、CDGF都是边长为1的正方形，M为棱AE上任意一点．（Ⅰ）若M为AE的中点，求证：AE⊥面MBC；
（Ⅱ）若M不为AE的中点，设二面角B-MC-A的大小为α，直线BE与平面BMC所成的角为β，求|
sin(β-
| ||
| cosα |
考点：直线与平面所成的角,直线与平面垂直的判定
专题：空间位置关系与距离,空间角
分析：（Ⅰ）根据AB=AE，M是AE的中点，推断出MB⊥AE，又有BC⊥AB，BC⊥BE，根据线面垂直的判定定理知BC⊥平面ABE，进而可知BC⊥AE，最后根据线面垂直的判定定理知．AE⊥平面MBC．
（Ⅱ）以B为原点，BA，BC，BE分别为x，y，z轴建立空间直角坐标系，设M的坐标，及平面MBC的法向量为
，根据
，推断出
，令x=λ-1，z=λ解得
，显然能求得平面MAC的法向量
，进而分别表示出sinβ和cosα，带入|
|即可．
（Ⅱ）以B为原点，BA，BC，BE分别为x，y，z轴建立空间直角坐标系，设M的坐标，及平面MBC的法向量为
| n |
|
|
| n |
| m |
sin(β-
| ||
| cosα |
解答：
解：（Ⅰ）∵AB=AE，M是AE的中点，
∴MB⊥AE，
又BC⊥AB，BC⊥BE，
∴BC⊥平面ABE，
∴BC⊥AE，
∴AE⊥平面MBC．
（Ⅱ）以B为原点，BA，BC，BE分别为x，y，z轴建立空间直角坐标系，
∵M在AE上，设M（λ，0，1-λ）（0≤λ≤1），
设平面MBC的法向量为
=（x，y，z），∵
，
∴
，令x=λ-1，z=λ，解得
=（λ-1，0，λ），
显然平面MAC的法向量
=（1，1，1），
∴|cosα|=
=
，
∴sinβ=
=
，
∴|
|=
=
=
∴MB⊥AE，
又BC⊥AB，BC⊥BE，
∴BC⊥平面ABE，
∴BC⊥AE，
∴AE⊥平面MBC．
（Ⅱ）以B为原点，BA，BC，BE分别为x，y，z轴建立空间直角坐标系，
∵M在AE上，设M（λ，0，1-λ）（0≤λ≤1），
设平面MBC的法向量为
| n |
|
∴
|
| n |
显然平面MAC的法向量
| m |
∴|cosα|=
|
| ||||
|
|
| |2λ-1| | ||||
|
∴sinβ=
|
| ||||
|
|
| |λ| | ||
|
∴|
sin(β-
| ||
| cosα |
| ||||
| cosα |
| ||||||||||||
|
| ||
| 2 |
点评：本题主要考查了线面垂直的判定定理，法向量的应用，以及三角函数恒等变换的应用．综合性强，计算量大，属于难度较大的题．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
如图，四棱锥P-ABCD的底面ABCD为矩形，且PA=AD=1，AB=2，∠PAB=120°，∠PBC=90°．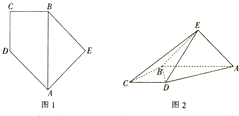
已知直角梯形ABCD的下底与等腰直角三角形ABE的斜边重合，AB⊥BC，且AB=2CD=2BC（如图1），将此图形沿AB折叠成直二面角，连接EC、ED，得到四棱锥E-ABCD（如图2）．